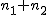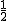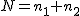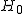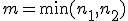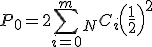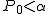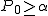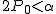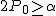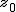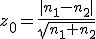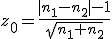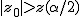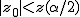[ ホーム | 一覧 | 検索 | 最終更新 | ヘルプ ] [ 新規 ]

健康統計の基礎・健康統計学 - 2009/13th/Wilcoxon のバックアップ(No.3)

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2009/13th/Wilcoxon へ行く。
- 1 (2009-07-12 (日) 07:43:34)
- 2 (2009-07-14 (火) 16:38:53)
- 3 (2009-07-15 (水) 14:28:54)
- 4 (2009-07-23 (木) 02:09:46)

ウィルコクソンの符号付順位検定

対応のある2つの標本について、それぞれのデータの対（各組）の差の順にもとづいて検定する
変数が順序尺度、もしくは、正規性があるか不明で間隔・比例尺度の場合に使うことができる

検定の対象

対応のある2組の標本（標本数は同じ）について考える。

2つの標本AとBについて、データを表にまとめると次のようになったとする。

	1	2	3	4	5	…	n-1	n
標本A	5	3	3	4	2	…	2	4
標本B	3	5	1	5	2	…	1	2

2つの標本のデータの各組を差の絶対値を求める
- 差が0の組は、この後の手続きから除外する
それぞれの差の絶対値に対応する組の数をもとに、差の絶対値の小さいほうから順位をつける
- 同一順位の場合は、次のように扱う（平均順位）
  - 2位が2つある場合：2位と3位の中間 (2+3)/2=2.5位を順位とする
  - 4位が3つある場合：4位と5位と6位の中間 (4+5+6)/3=5位を順位とする

	1	2	3	4	5	…	n-1	n
標本A	5	3	3	4	2	…	2	4
標本B	3	5	1	5	2	…	1	2
A-B	＋	−	＋	−	0	…	＋	＋

試行回数が $\normalsize n_1 + n_2$ と見なして考えると、2つの標本の中央値に差がないとすれば、「大きい」と「小さい」となる確率は $\normalsize \frac{1}{2}$ となるはず
標本数を $\normalsize N = n_1 + n_2$ とする

符号検定（小標本 : 二項検定を利用）

標本数が少ない場合は、二項検定を利用して、正確な有意確率を求める

帰無仮説と対立仮説

対応のある2組の標本の中央値に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の標本の中央値に差はない」
対立仮説 $\normalsize H_{1}$ は「2組の標本の中央値に差がある」

検定統計量の算出

試行回数が $\normalsize n_1 + n_2$ の状況で、帰無仮説が成り立つとすれば「大きい」と「小さい」となる確率は $\normalsize \frac{1}{2}$ となるのを利用
$\normalsize n_1$ と $\normalsize n_2$ の小さい方の値 $\normalsize m$ 以下に対応する符号が出現する確率を求める
$m = \min (n_1, n_2)$
二項検定を利用して、次の式から「 $\normalsize m$ 回以下」起きる確率を算出する
$P_0 = 2 \sum_{i=0}^m {}_N C_i \left( \frac{1}{2} \right)^2$

仮説の判定

算出した有意確率（P値）と有意水準を比較する
- 片側検定
  - 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize P_0 < \alpha$
  - 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize P_0 \geq \alpha$
- 両側検定
  - 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize 2P_0 < \alpha$
  - 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize 2P_0 \geq \alpha$

符号検定（大標本 : 標準正規分布を利用）

標本数が多い場合は、標準正規分布を利用して検定する

帰無仮説と対立仮説

対応のある2組の標本の中央値に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の標本の中央値に差はない」
対立仮説 $\normalsize H_{1}$ は「2組の標本の中央値に差がある」

検定統計量の算出

標準正規分布にしたがう、検定統計量 $\normalsize z_0$ を次の式から算出する
$z_0 = \frac{ | n_1 -n_2 | }{ \sqrt{ n_1 + n_2 } }$
二項分布は離散型の分布であるため、標準正規分布のような連続型の分布に近似すると、その精度はあまりよくない
そこで、Yatesの連続補正をすることで、精度をよくする
$z_0 = \frac{ | n_1 -n_2 | - 1 }{ \sqrt{ n_1 + n_2 } }$

仮説の判定（両側検定）

検定統計量 $\normalsize z_0$ と、有意水準 $\normalsize \alpha$ の有意点の値（標準正規分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |z_0| > z(\alpha/2)$
  - 「有意に差がある」「検定の結果、有意である」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |z_0| < z(\alpha/2)$
  - 「有意に差はない」「検定の結果、有意でない」「差があるとはいえない」

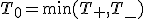$T_0 = \min ( T_{+} , T_{-})$

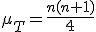$\mu_{T} = \frac{n(n+1)}{4}$

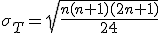$\sigma_{T} = \sqrt{ \frac{ n(n+1)(2n+1) }{24} }$

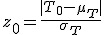$z_0 = \frac{ | T_0 - \mu_{T} | }{ \sigma_{T} }$

メニュー

授業内容

ケータイで教員にメール

mkawano%40ed.hyogo-dai.ac.jp

今日の5件

最新の10件

2024-07-12

2024-07-05

2024-06-28

2024-06-22

total: 32678
today: 1
yesterday: 0
now: 4