正規分布と関連する分布 - 健康統計の基礎・健康統計学

[ ホーム | 一覧 | 検索 | 最終更新 | ヘルプ ] [ 新規 | 編集 | 添付 ]

Top > 2009 > 8th > Normal_Distribution

正規分布と関連する分布

自然界や一般に観察できる多くのものの分布は、平均値を中心に左右対称の釣り鐘状の分布になっていることがある
- 生物現象、毎年の雨量など
- 身長や体重、標準的なテストの成績など

正規分布 (normal distribution)

正規分布とは

平均値を中心に左右対称の釣り鐘状になる分布を、「正規分布」という
$f(x) = \frac{1}{ \sqrt{2 \pi} \sigma } e^{ \frac{ (x - \mu)^2 }{ 2 \sigma^2 } }$
- $\normalsize \mu$ : 平均値
- $\normalsize \sigma$ : 標準偏差
- $\normalsize \sigma^2$ : 分散
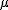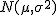確率密度関数が上の式になるとき、『 $\normalsize x$ は、平均が $\normalsize \mu$ で標準偏差が $\normalsize \sigma$ の正規分布にしたがう』といい、 $\normalsize N(\mu, \sigma^2)$ と表す
- つまり、平均値と分散（標準偏差）から分布が決まる
- さまざまな推定や検定に使われる

正規分布の特徴

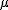分布の中心は平均値 $\normalsize \mu$ で、最も高い値（極大値）をとる
- 平均値が変化すると、分布が左右に移動する
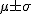$\normalsize \mu \pm \sigma$ で変曲点（曲線の凹凸の変わり目）になる
- 標準偏差が変化すると、分布の高さや広がりが変化する
平均値、中央値、最頻値は一致する
平均値と標準偏差から、分布の割合（曲線とx軸に囲まれる面積）が決まる
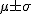- $\normalsize \mu \pm \sigma$ の範囲 : 全体の約 68.24%
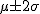- $\normalsize \mu \pm 2 \sigma$ の範囲 : 全体の約 95.44%
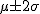- $\normalsize \mu \pm 2 \sigma$ の範囲 : 全体の約 97.73%
- それ以外の範囲 : 全体の約 0.27%

標準正規分布

標準正規分布とは

正規分布で、平均値が 0 、標準偏差が 1 になるように、変数 $\normalsize x$ を次のように変換する（変数変換）
$z = \frac{ x -\mu }{ \sigma }$
すると、標準偏差の式は次のようになる
$f(z) = \frac{1}{ \sqrt{2 \pi} } e^{ \frac{ z^2 }{ 2 } }$
確率密度関数が上の式になるとき、『 $\normalsize x$ は、標準正規分布にしたがう』という
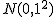- 『 $\normalsize x$ は、平均が 1 で標準偏差が 0 の正規分布にしたがう』ことになり、 $\normalsize N(0, 1^2)$ と表すことができる
- つまり、変数だけから分布が決まる
- さまざまな推定や検定に使われる

標準化（基準化）

先ほどの変数変換を、「標準化」まはた「基準化」という
$z = \frac{ x -\mu }{ \sigma }$
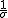（感覚としては）分布を平均値の分だけ 0 まで移動し、分散の広がりを $\normalsize \frac{1}{\sigma}$ にする
- 単位の異なるデータや平均値・分散が異なるデータを比較するときに使う（英語と数学のテストの成績の比較）
ちなみに偏差値は、標準化を応用したもので、次のような式になる
$z = 50 + 10 \times \frac{ x -\mu }{ \sigma }$

標準正規分布の特徴

基本的な特徴は、正規分布と同じ
確率密度関数とx軸で囲まれた面積は1で、面積は確率（割合）を表す

カイ二乗分布

カイ二乗分布とは

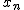変数 $\normalsize x_n$ が標準正規分布にしたがい、互いに独立であるとする
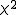次のようになるとき、『 $\normalsize x$ は、自由度 $\normalsize r$ のカイ二乗（ $\normalsize \chi^2$ ）分布にしたがう』という
$\chi^2 = {x_1}^2 + {x_2}^2 + \cdots + {x_n}^2 = \sum_{i=1}^n { x_i }^2$
- 自由度とは分布の形状に影響を及ぼす値で、自由度の値が変わると分布の形状も変化する

カイ二乗分布の特徴

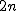平均は $\normalsize n$ 、分散は $\normalsize 2n$ になる
適合度や独立性の検定などに利用される
自由度が大きくなると、対称な分布に近づく

t分布

t分布とは

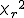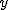標準正規分布にしたがう確率変数 $\normalsize x$ と、自由度 $\normalsize r$ のカイ二乗分布 $\normalsize {\chi_r}^2$ にしたがう確率変数 $\normalsize y$ があり、互いに独立であるとする
次のようになるとき、『 $\normalsize x$ は、自由度 $\normalsize r$ のt分布にしたがう』という
$t = \frac{ x }{ \sqrt{ \frac{ {\chi_r}^2 }{r} } }$
（感覚としては）正規分布に従う統計量を標準化したものの分布を表す

t分布の特徴

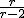平均は 0 、分散は $\normalsize \frac{r}{r-2}$ になる
自由度が大きくなると、標準正規分布に近づく
母平均の推定や検定、平均値の差の検定や検定など、多くの統計的推定で利用される

F分布

F分布とは

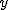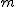確率変数 $\normalsize x$ と確率変数 $\normalsize y$ が、それぞれ自由度 $\normalsize m$ と $\normalsize n$ のカイ二乗分布にしたがい、互いに独立であるとする
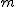次のようになるとき、『 $\normalsize x$ は、第一自由度が $\normalsize m$ で第二自由度が $\normalsize n$ のF分布にしたがう』という
$F = \frac{ {\chi_m}^2 }{m} \middle/ \frac{ {\chi_n}^2 }{n}$
（感覚としては）分散の比に対応する分布を表す

F分布の特徴

分散検定や分散分析（分散比の分布を調べる）に利用される
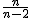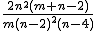平均は $\normalsize \frac{n}{n-2}$ 、分散は $\normalsize \frac{ 2n^2 (m+n-2) }{ m(n-2)^2 (n-4)}$ になる

メニュー

授業内容

ケータイで教員にメール

mkawano%40ed.hyogo-dai.ac.jp

今日の5件

最新の10件

2024-04-26

2024-04-19

2024-04-12

total: 1217
today: 1
yesterday: 0
now: 3

Last-modified: Tue, 11 Mar 2014 19:49:35 JST (3698d)