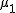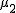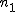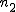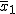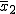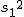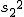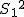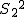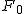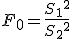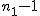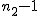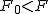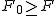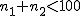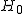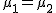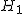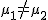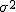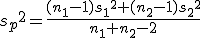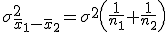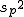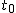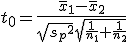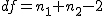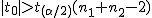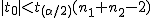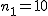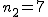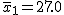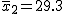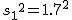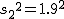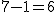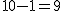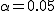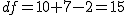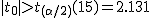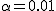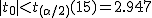対応のない2組の平均値の差の検定（母分散が未知だが等しい）

検定の対象

対応のない（独立した）2つの母集団について考える。それぞれの母数は次のとおり。ただし、母分散の値はわからない。

	母集団1	母集団2
母平均	$\normalsize \mu_1$	$\normalsize \mu_2$
標本の標本数	$\normalsize n_1$	$\normalsize n_2$
標本平均	$\normalsize \bar{x}_1$	$\normalsize \bar{x}_2$
標本分散	$\normalsize {s_1}^2$	$\normalsize {s_2}^2$

▲ ▼

等分散の検定（F検定）

まず、未知の2組の母分散が等しいかどうかを調べる。

2組の標本の不偏分散について、次のようにあらわす
- 値の大きいほうの標本 : 不偏分散 $\normalsize {S_1}^2$ 、標本数 $\normalsize n_1$
- 値の小さいほうの標本 : 不偏分散 $\normalsize {S_2}^2$ 、標本数 $\normalsize n_2$
F分布にしたがう、等分散の検定の検定統計量 $\normalsize F_0$ を次の式から算出する
$F_0 = \frac{ {S_1}^2 }{ {S_2}^2 }$
- この式は、標本分散の比率から母分散の比率を推測することを意味している
第1自由度が $\normalsize n_1 -1$ 、第2自由度が $\normalsize n_2 - 1$ 、有意水準 $\normalsize \alpha$ の有意点 F の値と、検定統計量を比較する
- $\normalsize F_0 < F$ ならば、母分散は未知で「等しい」
  → t検定で調べる
- $\normalsize F_0 \geq F$ ならば、母分散は未知で「等しくない」
  → Welchの検定で調べる

▲ ▼

t検定

標本数の和が $\normalsize n_1 + n_2 < 100$ の場合にも使われることがある

▲ ▼

帰無仮説と対立仮説

対応のない（独立した）2組の母集団の平均に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の母集団の平均に差はない」 : $\normalsize \mu_1 = \mu_2$
対立仮説 $\normalsize H_{1}$ は「2組の母集団の平均に差がある」 : $\normalsize \mu_1 \neq \mu_2$

▲ ▼

検定統計量の算出

標本分散から、全体の分散（母分散 $\normalsize \sigma^2$ の不偏推定量）を推測する
${s_p}^2 = \frac{(n_1 - 1){s_1}^2 + (n_2 - 1){s_2}^2}{ n_1 + n_2 -2 }$
標本平均の差の分散は、母分散を使って、次のように推測される
$\sigma_{ \bar{x}_1 - \bar{x}_2 }^2 = \sigma^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)$
母分散 $\normalsize \sigma^2$ を不偏推定量 $\normalsize {s_p}^2$ で代用し、t分布にしたがう、検定統計量 $\normalsize t_0$ を次の式から算出する
$t_0 = \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ {s_p}^2 } \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }$

▲ ▼

仮説の判定（両側検定）

検定統計量 $\normalsize t_0$ と、自由度 $\normalsize df = n_1 + n_2 -2$ 、有意水準 $\normalsize \alpha$ の有意点の値（t分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |t_0| > t_{(\alpha/2)}(n_1 + n_2 -2)$
  - 「有意に差がある」「検定の結果、有意である」「平均に差がある」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |t_0| < t_{(\alpha/2)}(n_1 + n_2 -2)$
  - 「有意に差はない」「検定の結果、有意でない」「平均に差があるとはいえない」

▲ ▼

例題

2つの銘柄のたばこのニコチン含有量について調べた結果、銘柄Aの10本については平均27.0mg、標準偏差1.7mgであった。また、銘柄Bの7本については平均29.3mg、標準偏差1.9mgであった。この2つの銘柄の間でニコチンの含有量に差はあるか？

▲ ▼

考え方

「銘柄A」のたばこと「銘柄B」について、それぞれの本数やニコチン含有量の平均と標準偏差についてまとめると、次の表のようになる。

	銘柄A	銘柄B
標本数	$\normalsize n_1 = 10$	$\normalsize n_2 = 7$
標本平均	$\normalsize \bar{x}_1 = 27.0$	$\normalsize \bar{x}_2 = 29.3$
標本分散	$\normalsize {s_1}^2 = 1.7^2$	$\normalsize {s_2}^2 =1.9 ^2$

まず、母分散が等しいかどうかを調べるため、等分散の検定をする。 F分布にしたがう、等分散の検定の検定統計量は、次のようになる。

$\begin{eqnarray}F_0 &=& \frac{ {1.9}^2 }{ {1.7}^2 } \\[10]&=& 1.2491\cdots \simeq 1.249\end{eqnarray}$

この値を、第1自由度が $\normalsize 7 -1 = 6$ 、第2自由度が $\normalsize 10 - 1 = 9$ 、有意水準 $\normalsize \alpha =0.05$ の F 値を分布表から調べると、3.374 となる。検定統計量と比較すると、 $\normalsize F_0 < F$ となり、 2組の標本の母分散は等分散であると判断できるので、t検定を用いる。

「銘柄A」のたばこと「銘柄B」について、ニコチン含有量の平均に差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「ニコチン含有量の平均に差はない」
対立仮説 $\normalsize H_{1}$ : 「ニコチン含有量の平均に差がある」

検定統計量を求めるため、まず、全体の分散（母分散 $\normalsize \sigma^2$ の不偏推定量）を求める。

$\begin{eqnarray}{s_p}^2 &=& \frac{(n_1 - 1){s_1}^2 + (n_2 - 1){s_2}^2}{ n_1 + n_2 -2 } \\[10]&=& \frac{(10 - 1){1.7}^2 + (7 - 1){1.9}^2}{ 10 + 7 -2 } \\[10]&=& \frac{ 9 \times 2.89 + 6 \times 3.61 }{ 15 } \\[10]&=& \frac{ 47.67 }{ 15 } = 3.178\end{eqnarray}$

したがって、検定統計量 $\normalsize t_0$ を求めると、次のようになる。

$\begin{eqnarray}t_0 &=& \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ {s_p}^2 } \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } } \\[10]&=& \frac{ 27.0 - 29.3 }{ \sqrt{ 3.178 } \sqrt{ \frac{1}{10} + \frac{1}{7} } } \\[10]&=& 2.6180 \simeq = 2.618\end{eqnarray}$

この検定統計量を両側検定で判定する。有意水準 $\normalsize \alpha =0.05$ では、自由度 $\normalsize df = 10 + 7 -2 = 15$ のt値を分布表から調べると、 $\normalsize |t_0| > t_{(\alpha/2)}(15) = 2.131$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 2つの銘柄のたばこのニコチン含有量には差がある。