健康統計の基礎・健康統計学 - 2009/3rd/Dispersion のバックアップ(No.5)
散布度(dispersion)
標準偏差偏差
分散(variance)と標準偏差(standard deviation)
不偏分散と不偏標準偏差
標準偏差の和n組の資料があるとき、資料全体の標準偏差は次のようになる。 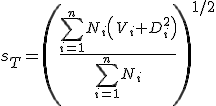
範囲
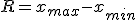 四分位偏差
四分位偏差=(第3四分位数-第1四分位数)/2 平均偏差
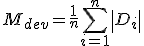 変異係数
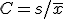
|
散布度(dispersion)
標準偏差偏差
分散(variance)と標準偏差(standard deviation)
不偏分散と不偏標準偏差
標準偏差の和n組の資料があるとき、資料全体の標準偏差は次のようになる。 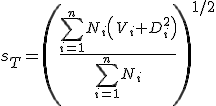
範囲
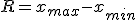 四分位偏差
四分位偏差=(第3四分位数-第1四分位数)/2 平均偏差
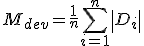 変異係数
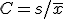
|