健康統計の基礎・健康統計学 - 2009/8th/Normal_Distribution のバックアップ(No.2)
正規分布と関連する分布
正規分布 (normal distribution)正規分布とは
正規分布の特徴
標準正規分布標準正規分布とは
標準化(基準化)
カイ二乗分布カイ二乗分布とは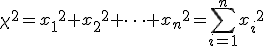 カイ二乗分布の特徴t分布t分布とは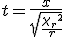 t分布の特徴F分布F分布とは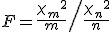 F分布の特徴 |
正規分布と関連する分布
正規分布 (normal distribution)正規分布とは
正規分布の特徴
標準正規分布標準正規分布とは
標準化(基準化)
カイ二乗分布カイ二乗分布とは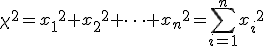 カイ二乗分布の特徴t分布t分布とは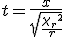 t分布の特徴F分布F分布とは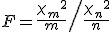 F分布の特徴 |