Top > 2009 > 7th > Expected_Value
AND OR

確率変数の期待値と分散

▲ ▼

期待値（平均値）

▲ ▼

期待値とは

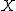  • 確率変数 \normalsize X の確率分布が次のようなとき、
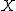    \normalsize X\normalsize x_1\normalsize x_2\normalsize \cdots\normalsize x_n計
    確率\normalsize p_1\normalsize p_2\normalsize \cdots\normalsize p_n1
  • 確率変数 \normalsize X の平均値、または期待値は、次のように表せる
    \mu = E(X) = x_1 p_1 + x_2 p_2 + \cdots + x_n p_n
  • 期待値とは、1回の試行の結果として期待される値の大きさを表す
▲ ▼

期待値の計算例

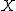  • サイコロを1回投げたときにでた目の数を確率変数 \normalsize X を使うと、その確率分布は次のようになる
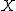    \normalsize X123456計
    確率\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize 1
  • 確率変数 \normalsize X の期待値（平均値）は、 \normalsize n = 6 なので、
    \begin{eqnarray}x_1 = 1, x_2 = 2, \cdots , x_6 = 6 \\[10]p_1 = \frac{1}{6}, p_2 = \frac{1}{6}, \cdots , p_6 = \frac{1}{6} \end{eqnarray}
  • したがって、次のようになる
    \begin{eqnarray}E(X) &=& 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + \cdots + 6 \times \frac{1}{6} \\[10]&=& \frac{21}{6} = 3.5\end{eqnarray}
▲ ▼

期待値と算術平均との関係

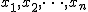  • n 個のデータ \normalsize x_1 , x_2 , \cdots , x_n の平均値は、次のように表せる
    \begin{eqnarray}\bar{x} &=& \frac{x_1 + x_2 + \cdots + x_n }{n} \\[10]&=& x_1 \times \frac{1}{n} + x_2 \times \frac{1}{n} + \cdots + x_n \times \frac{1}{n}\end{eqnarray}
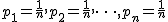  • ここで確率について、\normalsize p_1 = \frac{1}{n} , p_2 = \frac{1}{n} , \cdots , p_n = \frac{1}{n} とおく、つまり各々の確率が等しいと考えると、
    \begin{eqnarray}\bar{x} &=& x_1 p_1 + x_2 p_2 + \cdots + x_n p_n \\[10]&=& E(X)\end{eqnarray}
  • すなわち、各々の確率が等しくても等しくなくても、平均値（期待値）を求めることができる
▲ ▼

分散と標準偏差

▲ ▼

確率変数の分散と標準偏差

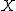  • 確率変数 \normalsize X の確率分布が次のようなとき、
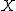    \normalsize X\normalsize x_1\normalsize x_2\normalsize \cdots\normalsize x_n計
    確率\normalsize p_1\normalsize p_2\normalsize \cdots\normalsize p_n1
  • 確率変数 \normalsize X の分散は次のように表す
    \begin{eqnarray}\sigma^2 = V(X) &=& (x_1 - \mu)^2 p_1 + (x_2 - \mu)^2 p_2 + \cdots + (x_n - \mu)^2 p_n \\[10]&=& \sum_{i=1}^{n} (x_i - \mu) p_i\end{eqnarray}
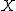  • 分散の正の平方根を、確率変数 \normalsize X の標準偏差といい、次のように表す
    \sigma = \sqrt{ V(X) }
▲ ▼

確率変数の分散と標準偏差の特徴

  • 分散や標準偏差が小さいほど、確率変数の値は平均に集中し、ばらつきが小さい
  • 分散や標準偏差が大きいほど、確率変数の値は平均から離れ、ばらつきが大きい
▲ ▼

確率変数の分散と標準偏差の計算

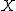  • サイコロを1回投げたときにでた目の数を確率変数 \normalsize X を使うと、その確率分布は次のようになる
    \normalsize X123456計
    確率\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize \frac{1}{6}\normalsize 1
  • したがって、分散は次のようにして求められる
    \begin{eqnarray}\sigma^2 = V(X) &=& (1 - 3.5)^2 \times \frac{1}{6} + (2 - 3.5)^2 \times \frac{1}{6} + \cdots + (6 - 3.5)^2 \times \frac{1}{6} \\[10]&=& \frac{35}{12} \simeq 2.92\end{eqnarray}
  • また、標準偏差は次のようになる
    \begin{eqnarray}\sigma &=& \sqrt{ V(X) } \\[10]&=& \sqrt{ \frac{35}{12} } \simeq 1.71\end{eqnarray}
  • つまり、サイコロを何回も投げたとき、そのでた目の平均が 3.5 ± 1.71 （1.79〜5.21）の範囲になる確率が高いことを示している
リロード   差分   ホーム 一覧 検索 最終更新 バックアップ リンク元   ヘルプ   最終更新のRSS
Last-modified: Tue, 11 Mar 2014 19:49:35 JST (3698d)