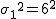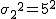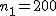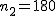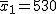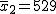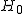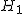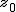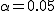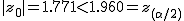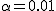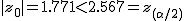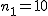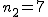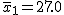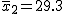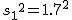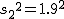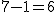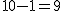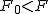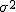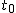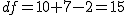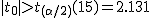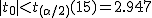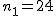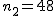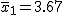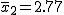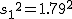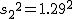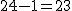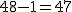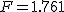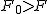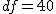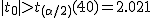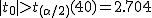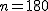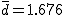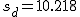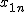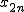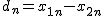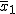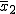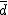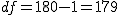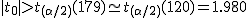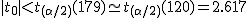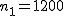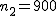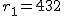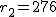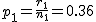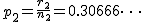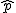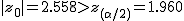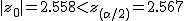2010/14th/Example のバックアップ(No.1) - 健康統計の基礎・健康統計学

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2010/14th/Example へ行く。
- 1 (2010-07-28 (水) 02:23:50)

2つの標本の仮設検定の例題

対応のない2組の平均値の差の検定（母分散が既知）

例題

ある製品の製造工程で、ある1週間に製造された製品200個の重さの平均は530g、標準偏差は6gであった。次の1週間に製造された製品180個の重さの平均は529g、標準偏差は5gであった。これらの結果から、それぞれの週に作られた製品の重さの平均に差はあるか？

▲ ▼

考え方

「ある1週間」と「次の1週間」について、それぞれの製品の個数や重さの平均と標準偏差についてまとめると、次の表のようになる。なお、標本標準偏差の二乗が母分散と同じだと見なすことにする。

	ある1週間に製造された製品	次の1週間に製造された製品
母分散	$\normalsize {\sigma_1}^2 = 6^2$	$\normalsize {\sigma_2}^2 = 5^2$
標本の標本数	$\normalsize n_1 = 200$	$\normalsize n_2 = 180$
標本平均	$\normalsize \bar{x}_1 = 530$	$\normalsize \bar{x}_2 = 529$

それぞれの週に製造された製品の重さの平均に差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「それぞれの週に製造された製品の重さの平均に差はない」
対立仮説 $\normalsize H_{1}$ : 「それぞれの週に製造された製品の重さの平均に差がある」

上の表にまとめた情報から、検定統計量 $\normalsize z_0$ を求める。

$\begin{eqnarray}z_0 &=& \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ \frac{ {\sigma_1}^2 }{n_1} + \frac{ {\sigma_2}^2 }{n_2} } } \\[10]&=& \frac{ 530 - 529 }{ \sqrt{ \frac{ {6}^2 }{ 200 } + \frac{ { 5 }^2 }{ 180 } } } \\[10]&=& 1.7708\cdots \\[10] &\simeq& 1.771\end{eqnarray}$

この検定統計量を両側検定で判定すると、有意水準 $\normalsize \alpha =0.05$ では、 $\normalsize |z_0| = 1.771 < 1.960 = z_{(\alpha/2)}$ となり、帰無仮説は棄却できない。つまり、有意水準 5% で仮説検定を行った結果、 それぞれの週に製造した製品の重さの平均に差があるとはいえない。

なお、有意水準 $\normalsize \alpha =0.01$ でも、 $\normalsize |z_0| = 1.771 < 2.567 = z_{(\alpha/2)}$ となり、帰無仮説は棄却できない。

▲ ▼

対応のない2組の平均値の差の検定（母分散が未知だが等しい）

▲ ▼

例題

2つの銘柄のたばこのニコチン含有量について調べた結果、銘柄Aの10本については平均27.0mg、標準偏差1.7mgであった。また、銘柄Bの7本については平均29.3mg、標準偏差1.9mgであった。この2つの銘柄の間でニコチンの含有量に差はあるか？

▲ ▼

考え方

「銘柄A」のたばこと「銘柄B」について、それぞれの本数やニコチン含有量の平均と標準偏差についてまとめると、次の表のようになる。

	銘柄A	銘柄B
標本数	$\normalsize n_1 = 10$	$\normalsize n_2 = 7$
標本平均	$\normalsize \bar{x}_1 = 27.0$	$\normalsize \bar{x}_2 = 29.3$
標本分散	$\normalsize {s_1}^2 = 1.7^2$	$\normalsize {s_2}^2 =1.9 ^2$

まず、母分散が等しいかどうかを調べるため、等分散の検定をする。 F分布にしたがう、等分散の検定の検定統計量は、次のようになる。

$\begin{eqnarray}F_0 &=& \frac{ {1.9}^2 }{ {1.7}^2 } \\[10]&=& 1.2491\cdots \simeq 1.249\end{eqnarray}$

この値を、第1自由度が $\normalsize 7 -1 = 6$ 、第2自由度が $\normalsize 10 - 1 = 9$ 、有意水準 $\normalsize \alpha =0.05$ の F 値を分布表から調べると、3.374 となる。検定統計量と比較すると、 $\normalsize F_0 < F$ となり、 2組の標本の母分散は等分散であると判断できるので、t検定を用いる。

「銘柄A」のたばこと「銘柄B」について、ニコチン含有量の平均に差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「ニコチン含有量の平均に差はない」
対立仮説 $\normalsize H_{1}$ : 「ニコチン含有量の平均に差がある」

検定統計量を求めるため、まず、全体の分散（母分散 $\normalsize \sigma^2$ の不偏推定量）を求める。

$\begin{eqnarray}{s_p}^2 &=& \frac{(n_1 - 1){s_1}^2 + (n_2 - 1){s_2}^2}{ n_1 + n_2 -2 } \\[10]&=& \frac{(10 - 1){1.7}^2 + (7 - 1){1.9}^2}{ 10 + 7 -2 } \\[10]&=& \frac{ 9 \times 2.89 + 6 \times 3.61 }{ 15 } \\[10]&=& \frac{ 47.67 }{ 15 } = 3.178\end{eqnarray}$

したがって、検定統計量 $\normalsize t_0$ を求めると、次のようになる。

$\begin{eqnarray}t_0 &=& \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ {s_p}^2 } \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } } \\[10]&=& \frac{ 27.0 - 29.3 }{ \sqrt{ 3.178 } \sqrt{ \frac{1}{10} + \frac{1}{7} } } \\[10]&=& 2.6180 \simeq = 2.618\end{eqnarray}$

この検定統計量を両側検定で判定する。有意水準 $\normalsize \alpha =0.05$ では、自由度 $\normalsize df = 10 + 7 -2 = 15$ のt値を分布表から調べると、 $\normalsize |t_0| > t_{(\alpha/2)}(15) = 2.131$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 2つの銘柄のたばこのニコチン含有量には差がある。

なお、有意水準 $\normalsize \alpha =0.01$ では、 $\normalsize |t_0| < t_{(\alpha/2)}(15) = 2.947$ となり、帰無仮説は棄却できない。つまり、有意水準 1% では、2つの銘柄のたばこのニコチン含有量には差があるとはいえない。

▲ ▼

対応のない2組の平均値の差の検定（母分散が未知で等しくない）

▲ ▼

例題

女子大生に、デートに臨むときのハイヒールの高さを聞いたところ、自分を「おしゃれ」と答えた24人のハイヒールの高さの平均は3.67cm、標準偏差は1.79cmであった。また、自分を「普通」と答えた48人のハイヒールの高さの平均は2.77cm、標準偏差は1.29cmであった。「おしゃれ」と答えた人たちと「普通」と答えた人たちとでハイヒールの高さに差はあるか？

▲ ▼

考え方

自分を「おしゃれ」と答えた女子大生と自分を「普通」と答えた女子大生のハイヒールの高さについて、答えた人数やハイヒールの高さの平均と標準偏差についてまとめると、次の表のようになる。

	銘柄A	銘柄B
標本数	$\normalsize n_1 = 24$	$\normalsize n_2 = 48$
標本平均	$\normalsize \bar{x}_1 = 3.67$	$\normalsize \bar{x}_2 = 2.77$
標本分散	$\normalsize {s_1}^2 = 1.79^2$	$\normalsize {s_2}^2 =1.29 ^2$

まず、母分散が等しいかどうかを調べるため、等分散の検定をする。 F分布にしたがう、等分散の検定の検定統計量は、次のようになる。

$\begin{eqnarray}F_0 &=& \frac{ {1.79}^2 }{ {1.29}^2 } \\[10]&=& 1.92542\cdots \simeq 1.925\end{eqnarray}$

この値を、第1自由度が $\normalsize 24 -1 = 23$ 、第2自由度が $\normalsize 48 - 1 = 47$ 、有意水準 $\normalsize \alpha =0.05$ の F 値を分布表から調べると、 $\normalsize F=1.761$ となる。検定統計量と比較すると、 $\normalsize F_0 > F$ となり、 2組の標本の母分散は等分散ではないと判断できるので、Welchの検定を用いる。

t分布にしたがう検定統計量 $\normalsize t_0$ を求めると、次のようになる。

$\begin{eqnarray}t_0 &=& \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} } } \\[10]&=& \frac{ 3.67 - 2.77 }{ \sqrt{ \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} } } \\[10]&=& \frac{ 3.67 - 2.77 }{ \sqrt{ \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} } } \\[10]&=& 2.82552 \simeq 2.826\end{eqnarray}$

次に、検定のための自由度を求める。

$\begin{eqnarray}df &=& \left( \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} \right)^2 \div \left\{ \frac{ \left( \frac{ {s_1}^2 }{n_1} \right)^2 }{n_1 - 1} + \frac{ \left( \frac{ {s_2}^2 }{n_2} \right)^2 }{n_2 - 1} \right\} \\[10]&=& \left( \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} \right)^2 \div \left\{ \frac{ \left( \frac{ {1.79}^2 }{24} \right)^2 }{24 - 1} + \frac{ \left( \frac{ {1.29}^2 }{48} \right)^2 }{48 - 1} \right\} \\[10]&=& 40.019\end{eqnarray}$

整数分だけを自由度として採用すると、 $\normalsize df = 40$ となる。

この検定統計量を両側検定で判定する。有意水準 $\normalsize \alpha =0.05$ では、自由度 $\normalsize df = 40$ のt値を分布表から調べると、 $\normalsize |t_0| > t_{(\alpha/2)}(40) = 2.021$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 「おしゃれ」と答えた人たちと「普通」と答えた人たちとでハイヒールの高さに差がある。

なお、有意水準 $\normalsize \alpha =0.01$ では、 $\normalsize |t_0| > t_{(\alpha/2)}(40) = 2.704$ となり、やはり帰無仮説は棄却される。

▲ ▼

対応のある2組の平均値の差の検定

▲ ▼

例題

街頭で180人の人に「体重を教えてください」と声をかけたときに、答えた体重と本当の体重の差にについて、その差の平均は1.676kg、差の標準偏差は10.218kgであった。このとき、街頭で声をかけられて答えた体重と本当の体重に差はあるか？

▲ ▼

考え方

街頭で声をかけて答えた体重と本当の体重について、答えた人数や体重の平均と差の標準偏差についてまとめると、次の表のようになる。

	回答された体重
標本数	$\normalsize n = 180$
差の平均	$\normalsize \bar{d} = 1.676$
差の標準偏差	$\normalsize s_d = 10.218$

街頭で声をかけて答えた体重と本当の体重について差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「街頭で声をかけて答えた体重と本当の体重に差はない」
対立仮説 $\normalsize H_{1}$ : 「街頭で声をかけて答えた体重と本当の体重に差がある」

差の平均は、次のように、対応するデータ同士の差を求めて、その合計を標本数で割ったものになる。

	答えた体重	本当の体重	差
回答1	55kg	60kg	-5
回答2	52kg	56.5kg	-4.5
回答3	63kg	61kg	2
回答4	78	74	4
	…	…	…
回答 n	$\normalsize x_{1n}$	$\normalsize x_{2n}$	$\normalsize d_n = x_{1n} - x_{2n}$
平均	$\normalsize \bar{x}_1$	$\normalsize \bar{x}_2$	$\normalsize \bar{d}$

t分布にしたがう検定統計量 $\normalsize t_0$ を求めると、次のようになる。

$\begin{eqnarray}t_0 &=& \frac{ \bar{d} }{ \frac{s_d}{ \sqrt{n} } } \\[10]&=& \frac{ 1.676 }{ \frac{10.218}{ \sqrt{180} } } \\[10]&=& 2.20062\cdots = 2.201\end{eqnarray}$

この検定統計量を両側検定で判定する。有意水準 $\normalsize \alpha =0.05$ では、自由度 $\normalsize df = 180 - 1 = 179$ のt値を分布表から調べると、該当する自由度がないため、最も近い自由度120のときのt値を読み取ると、 $\normalsize |t_0| > t_{(\alpha/2)}(179) \simeq t_{(\alpha/2)}(120) = 1.980$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 街頭で声をかけてときに答えた体重と本当の体重には差がある。

なお、有意水準 $\normalsize \alpha =0.01$ では、該当する自由度がないため、最も近い自由度120のときのt値を読み取ると、 $\normalsize |t_0| < t_{(\alpha/2)}(179) \simeq t_{(\alpha/2)}(120) = 2.617$ となり、帰無仮説は棄却できない。つまり、有意水準 1% では、街頭で声をかけてときに答えた体重と本当の体重には差があるとはいえない。

▲ ▼

比率の差の検定

▲ ▼

例題

男性有権者の中から1,200人、女性有権者の中から900人を選んで、内閣の支持者の数を調べた結果、それぞれ432人と276人であった。男性と女性間で支持率に差があるといえるか？

▲ ▼

考え方

男女それぞれ有権者について、それぞれの人数や支持者の数についてまとめると、次の表のようになる。

	男性有権者	女性有権者
標本数	$\normalsize n_1 =1200$	$\normalsize n_2 = 900$
事象が起こる数	$\normalsize r_1 =432$	$\normalsize r_2 =276$
標本比率	$\normalsize p_1 = \frac{r_1}{n_1} = 0.36$	$\normalsize p_2 = \frac{r_2}{n_2} = 0.30666\cdots$

男女それぞれ有権者について、内閣支持率に差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「男性と女性とで内閣支持率に差はない」
対立仮説 $\normalsize H_{1}$ : 「男性と女性とで内閣支持率に差がある」

まず、母比率の推定値 $\normalsize \hat{p}$ を求める

$\begin{eqnarray}\hat{p} &=& \frac{ n_1 p_1 + n_2 p_2 }{ n_1 + n_2 } \\[10]&=& \frac{ 1200 \times 0.36 + 900 \times 0.30666\cdots }{ 1200 + 900 } \\[10]&=& \frac{ 432 + 276 }{ 2100 } = 0.33714\cdots \simeq 0.3371\end{eqnarray}$

したがって、検定統計量 $\normalsize z_0$ を求めると、次のようになる。

$\begin{eqnarray}z_0 &=& \frac{ p_1 - p_2 }{ \sqrt{ \hat{p} ( 1 - \hat{p} ) \left( \frac{1}{n_1} + \frac{1}{n_2} \right) } } \\[10]&=& \frac{ 0.36 - 0.30666\cdots }{ \sqrt{ 0.3371 \times ( 1 - 0.3371 ) \left( \frac{1}{1200} + \frac{1}{900} \right) } } \\[10]&=& 2.55849\cdots \simeq 2.558 \end{eqnarray}$

この検定統計量を両側検定で判定すると、有意水準 $\normalsize \alpha =0.05$ では、 $\normalsize |z_0| = 2.558 > z_{(\alpha/2)} = 1.960$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 男性と女性とで内閣支持率に差がある。

なお、有意水準 $\normalsize \alpha =0.01$ では、 $\normalsize |z_0| = 2.558 < z_{(\alpha/2)} = 2.567$ となり、帰無仮説は棄却できない。つまり、男性と女性とで内閣支持率に差があるとはいえない。

メニュー

授業内容

ケータイで教員にメール

健康統計の基礎・健康統計学 - 2010/14th/Example のバックアップ(No.1)