代表値(average)
- データの分布などの特徴を示す数値(特性値)を「代表値」という。
- データ全体をひとつの値で代表させる値である。
平均値(mean)
算術平均(arithmetic mean)
- 算術平均
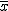 は、データをすべて足しあわせ、データ数で割ったもの。 は、データをすべて足しあわせ、データ数で割ったもの。
- 平均値のなかで、もっとも一般的なもの。
幾何平均(geometric mean)
- 幾何平均
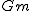 は、各データの値の積に対してデータ数のべき根を求めたもの。 は、各データの値の積に対してデータ数のべき根を求めたもの。
- 幾何平均の例
- 5年間の物価上昇率が7%のとき、1年の平均上昇率は何%か?
- 過去3年間の売上高の対前年比が120%、110%、130%のとき、平均の売上高の伸びは?
調和平均(harmonic mean)
- 調和平均
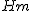 は、データ数を各データの値の逆数の和で割ったもの。 は、データ数を各データの値の逆数の和で割ったもの。
- 調和平均の例
- 山頂まで6kmの道のりを、往きは2km/hで、帰りは6km/hで歩いたとき、平均の速さはいくらか?
- 車でドライブをして、最初の24kmは30km/h、次の24kmは40km/h、最後の24kmは60km/hで走った時、平均速度はいくらか?
中央値(median)
中央値(中位数)
- 中央値
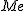 は、データを大きさの順に並べたときに、中央にくる値のことである。 は、データを大きさの順に並べたときに、中央にくる値のことである。
- データ数が奇数のときは中央にくるデータの値になる。
- データ数が偶数のときは中央にある2つのデータの平均の値になる。
- 中央に位置するデータが複数個ある場合(「結び(tie)」があるという)、次のような式で中央値を求めることができる。
- 中央にあるデータ :
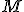
- 値
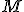 になるデータの個数 : になるデータの個数 : 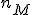
- 値
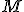 より小さいデータの個数 : より小さいデータの個数 : 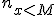
- 値
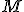 より大きいデータの個数 : より大きいデータの個数 : 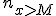
- 度数分布表がある場合は、階級や度数などの情報から、中央値を求めることもできる。
- 標本数 :

- 階級幅 :
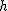
- m 番目の階級の下限 :
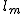
- m 番目の階級の度数 :
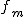
- m-1 番目までの累積度数 :
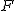
四分位数(quartile)
- ヒストグラムから考えると、四分位数はヒストグラムの面積を1/4ずつに分ける値である。
- 中央値は、ヒストグラムの面積を半分に分ける値になる。
- データを大きさの順に並べた場合は、データの個数を4分の1ずつの部分にわける個所である。
- 小さいほうから、第1、第2、第3四分位数といい、中央値は、第2四分位数になる。
- データが
 個のあるときの第1四分位数 個のあるときの第1四分位数 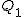 と第3四分位数 と第3四分位数 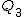 は、次のようにして求められる。 は、次のようにして求められる。
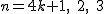 の場合 の場合
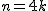 の場合 の場合
百分位数(percentile)
- 百分位数(パーセンタイル値)は、ヒストグラムの面積を1/100ずつに分ける値である。
- 25パーセンタイル値は第1四分位数である。
- 50パーセンタイル値は中央値(第2四分位数でもある)。
- 度数分布表がある場合は、階級や度数などからパーセンタイル値
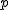 を求めることもできる。 を求めることもできる。
- 標本数 :

- 階級幅 :
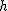
- m 番目の階級の下限 :
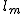
- m 番目の階級の度数 :
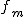
- m-1 番目までの累積度数 :
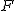
最頻値(mode)
- 最頻値
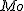 は、データのなかで最も多く出てくる値のことである。 は、データのなかで最も多く出てくる値のことである。
- 度数分布表がある場合は、もっとも度数の多い階級値を最頻値として、次の式から最頻値を求めることができる。
- 最大度数の階級 :
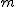
- 階級幅 :
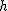
- m 番目の階級の下限 :
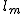
- m 番目の階級の度数 :
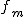
- 分布が釣り鐘形の場合は、ピアソン(Pearson)の式を用いることができる。
代表値の特性
- 平均値はすべてのデータを反映している。
- ハズレ値(極端に小さく・大きくて飛び離れたデータ)があるとその影響を受けやすいため、ハズレ値の考慮が必要。
- 中央値(四分位数や百分位数も)は分布上の位置(中央など)を示す。
- ハズレ値の影響を受けにくく、分布に偏りがある場合に優れている。
- 最頻値は、「データの多くはこのあたりにある」という説明をするのにわかりやすい。
|
|