確率変数の期待値と分散
期待値(平均値)
期待値とは
- 確率変数
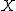 の確率分布が次のようなとき、 の確率分布が次のようなとき、
- 確率変数
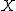 の平均値、または期待値は、次のように表せる の平均値、または期待値は、次のように表せる
- 期待値とは、1回の試行の結果として期待される値の大きさを表す
期待値の計算例(1)
- サイコロを1回投げたときにでた目の数を確率変数
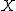 を使うと、その確率分布は次のようになる を使うと、その確率分布は次のようになる
- 確率変数
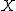 の期待値(平均値)は、 の期待値(平均値)は、  なので、 なので、
- したがって、次のようになる
- つまり、サイコロを何回も投げたときに、でた目の平均をとると 3.5 になることを示している
期待値の計算例(2)
- サイコロを5回連続で投げたときに1の目が出る回数を確率変数
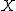 とすると、その確率分布は次のようになる とすると、その確率分布は次のようになる
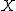 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|
| 確率 | 0.4019 | 0.4019 | 0.1608 | 0.0322 | 0.0032 | 0.0001 |
|---|
- 確率変数
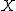 の期待値(平均値)は、 の期待値(平均値)は、  なので、 なので、
- したがって、次のようになる
- つまり、サイコロを5回連続投げて1の目が出るのは1回あるかないか程度であることを示している
期待値の計算例(3)
- 宝くじの期待値を求めることもできる。宝くじの場合は「当せん金×当せん確率」の合計が期待値となる。
- 例えば、平成21年年末ジャンボ宝くじは、1ユニット(1000万枚)あたり、次のような当せん本数になっている。なお、当せん確率は「当せん本数÷1000万×100」から求めている。
| 等級 | 当せん金 | 当せん本数 | 当せん確率 |
|---|
| 1等 | 200,000,000円 | 1本 | 0.00001% | | 1等前後賞 | 50,000,000円 | 2本 | 0.00002% | | 1等組違い賞 | 100,000円 | 99本 | 0.00099% | | 2等 | 100,000,000円 | 2本 | 0.00002% | | 3等 | 5,000,000円 | 10本 | 0.0001% | | 4等 | 100,000円 | 600本 | 0.006% | | 5等 | 10,000円 | 10,000本 | 0.1% | | 6等 | 3,000円 | 100,000本 | 1% | | 7等 | 300円 | 1,000,000本 | 10% | | 元気に2010年賞 | 1,000,000円 | 100本 | 0.001% |
- 宝くじがいくら当たるかの期待値を調べるには、「当せん金×当せん確率」の合計を求めるので、
- つまり、宝くじ1枚(300円)を買うと、1枚につき141.99円の還元が期待できる、ということを示している。
期待値と算術平均との関係
- n 個のデータ
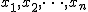 の平均値は、次のように表せる の平均値は、次のように表せる
- ここで確率について、
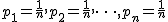 とおく、つまり各々の確率が等しいと考えると、 とおく、つまり各々の確率が等しいと考えると、
- すなわち、各々の確率が等しくても等しくなくても、平均値(期待値)を求めることができる
分散と標準偏差
確率変数の分散と標準偏差
- 確率変数
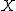 の確率分布が次のようなとき、 の確率分布が次のようなとき、
- 確率変数
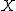 の分散は次のように表す の分散は次のように表す
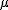 は期待値 は期待値 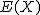 簡単に表したもの 簡単に表したもの- 分散の正の平方根を、確率変数
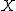 の標準偏差といい、次のように表す の標準偏差といい、次のように表す
確率変数の分散と標準偏差の特徴
- 分散や標準偏差が小さいほど、確率変数の値は平均に集中し、ばらつきが小さい
- 分散や標準偏差が大きいほど、確率変数の値は平均から離れ、ばらつきが大きい
- 分散は変数の単位の2乗を表す(例えば変数の単位がcmなら、分散の単位cm^2)ため、元の単位と同じ標準偏差を用いて平均からのばらつきを表す
確率変数の分散と標準偏差の計算
- サイコロを1回投げたときにでた目の数を確率変数
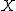 を使うと、その確率分布は次のようになる を使うと、その確率分布は次のようになる
- したがって、分散は次のようにして求められる
- また、標準偏差は次のようになる
- つまり、サイコロを何回も投げたとき、そのでた目の平均が 3.5 ± 1.71 (1.79〜5.21)の範囲になる確率が高いことを示している
|
|