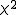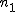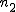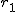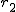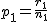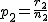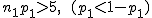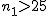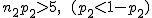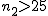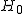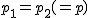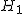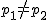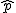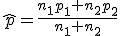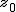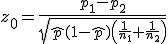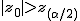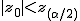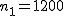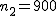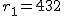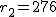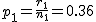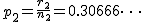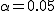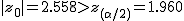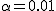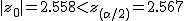比率の差の検定

比率の差の検定には、次の2つの方法がある。

正規分布に近似して検定
独立性の検定（ $\normalsize \chi^2$ 検定）

ここでは、正規分布に近似する方法を説明する。

検定の対象

2組の標本のについて考える。それぞれの統計量は次のとおり。

	標本1	標本2
標本数	$\normalsize n_1$	$\normalsize n_2$
事象が起こる回数	$\normalsize r_1$	$\normalsize r_2$
標本比率	$\normalsize p_1 = \frac{r_1}{n_1}$	$\normalsize p_2 = \frac{r_2}{n_2}$

▲ ▼

正規分布に近似する方法

この方法を使って、標本比率の差を検定するには、次の2つの条件を満たさないといけない

$\normalsize n_1 p_1 > 5 , \hspace{8} (p_1 < 1 - p_1)$ 、または $\normalsize n_1 > 25$
$\normalsize n_2 p_2 > 5 , \hspace{8} (p_2 < 1 - p_2)$ 、または $\normalsize n_2 > 25$

▲ ▼

帰無仮説と対立仮説

2組の標本の比率に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の標本の比率に差はない」 : $\normalsize p_1 = p_2 (= p)$
対立仮説 $\normalsize H_{1}$ は「2組の標本の比率に差がある」 : $\normalsize p_1 \neq p_2$

▲ ▼

検定統計量の算出

母比率の推定値 $\normalsize \hat{p}$ を求める
$\hat{p} = \frac{ n_1 p_1 + n_2 p_2 }{ n_1 + n_2 }$
標準正規分布にしたがう、検定統計量 $\normalsize z_0$ を次の式から算出する
$z_0 = \frac{ p_1 - p_2 }{ \sqrt{ \hat{p} ( 1 - \hat{p} ) \left( \frac{1}{n_1} + \frac{1}{n_2} \right) } }$

▲ ▼

仮説の判定（両側検定）

検定統計量 $\normalsize z_0$ と、有意水準 $\normalsize \alpha$ の有意点の値（標準正規分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |z_0| > z_{(\alpha/2)}$
  - 「有意に差がある」「検定の結果、有意である」「比率に差がある」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |z_0| < z_{(\alpha/2)}$
  - 「有意に差はない」「検定の結果、有意でない」「比率に差があるとはいえない」

▲ ▼

例題

男性有権者の中から1,200人、女性有権者の中から900人を選んで、内閣の支持者の数を調べた結果、それぞれ432人と276人であった。男性と女性間で支持率に差があるといえるか？

▲ ▼

考え方

男女それぞれ有権者について、それぞれの人数や支持者の数についてまとめると、次の表のようになる。

	男性有権者	女性有権者
標本数	$\normalsize n_1 =1200$	$\normalsize n_2 = 900$
事象が起こる数	$\normalsize r_1 =432$	$\normalsize r_2 =276$
標本比率	$\normalsize p_1 = \frac{r_1}{n_1} = 0.36$	$\normalsize p_2 = \frac{r_2}{n_2} = 0.30666\cdots$

男女それぞれ有権者について、内閣支持率に差があるかどうか調べたいので、帰無仮説と対立仮説は、次のようになる。

帰無仮説 $\normalsize H_{0}$ : 「男性と女性とで内閣支持率に差はない」
対立仮説 $\normalsize H_{1}$ : 「男性と女性とで内閣支持率に差がある」

まず、母比率の推定値 $\normalsize \hat{p}$ を求める

$\begin{eqnarray}\hat{p} &=& \frac{ n_1 p_1 + n_2 p_2 }{ n_1 + n_2 } \\[10]&=& \frac{ 1200 \times 0.36 + 900 \times 0.30666\cdots }{ 1200 + 900 } \\[10]&=& \frac{ 432 + 276 }{ 2100 } = 0.33714\cdots \simeq 0.3371\end{eqnarray}$

したがって、検定統計量 $\normalsize z_0$ を求めると、次のようになる。

$\begin{eqnarray}z_0 &=& \frac{ p_1 - p_2 }{ \sqrt{ \hat{p} ( 1 - \hat{p} ) \left( \frac{1}{n_1} + \frac{1}{n_2} \right) } } \\[10]&=& \frac{ 0.36 - 0.30666\cdots }{ \sqrt{ 0.3371 \times ( 1 - 0.3371 ) \left( \frac{1}{1200} + \frac{1}{900} \right) } } \\[10]&=& 2.55849\cdots \simeq 2.558 \end{eqnarray}$

この検定統計量を両側検定で判定すると、有意水準 $\normalsize \alpha =0.05$ では、 $\normalsize |z_0| = 2.558 > z_{(\alpha/2)} = 1.960$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 男性と女性とで内閣支持率に差がある。