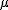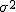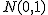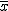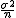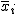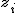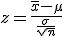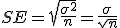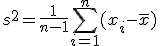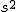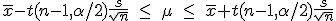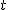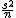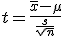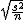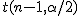2010/11th/Population_Mean のバックアップ(No.2) - 健康統計の基礎・健康統計学

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2010/11th/Population_Mean へ行く。
- 1 (2010-06-30 (水) 13:49:29)
- 2 (2010-06-30 (水) 15:38:29)
- 3 (2010-07-07 (水) 01:00:36)

母平均の区間推定

母集団から抽出した標本をもとに母集団の平均（母平均）を区間推定する

大卒100人の初任給のデータからすべての大卒の初任給の平均を推定
あるクラスの男子の身長のデータから日本全体の同年代の男子の身長の平均を推定

▲ ▼

母平均の区間推定の準備

▲ ▼

標準得点

平均が 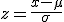$\normalsize \mu$ 、分散が $\normalsize \sigma^2$ の 正規分布から、 標準正規分布を導くときに、次の式を用いて標準化を行う。

$z = \frac{ x - \mu }{ \sigma }$

このときの $\normalsize z$ を、 標準得点（standardized score）という。標準得点は、平均が0で分散が1の標準正規分布 $\normalsize N(0,1)$ にしたがう。

▲ ▼

中心極限定理と標本平均の分布

中心極限定理では、「平均が $\normalsize \mu$ で分散が $\normalsize \sigma^2$ の母集団について、母集団の分布が正規分布でなくても、標本の大きさ $\normalsize n$ が十分大きい標本を抽出すれば、標本平均 $\normalsize \bar{x}$ の分布は平均が $\normalsize \mu$ で分散が $\normalsize \frac{\sigma^2}{n}$ の正規分布にしたがう」ことが成り立つ。

ある標本の標本平均 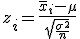$\normalsize \bar{x}_i$ を標準化した分布を考える。標本平均を標準得点 $\normalsize z_i$ に変換すると、次の式になる。

$z_i = \frac{ \bar{x}_i - \mu }{ \sqrt{ \frac{\sigma^2}{n} } }$

▲ ▼

標本平均の分布と信頼区間

標準正規分布にしたがう標本平均の信頼区間について考える。

95%信頼区間は、標本平均を標準化した $\normalsize z$ が、

1.96〜1.96の区間を示す。

つまり、信頼度を95%とした95%信頼区間では、標本平均の存在する範囲は次の式のようになる。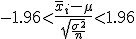

$-1.96 < \frac{ \bar{x}_i - \mu }{ \sqrt{ \frac{\sigma^2}{n} } } < 1.96$

ここで、信頼度を 100(1-α)% とすると、次のように書き換えることができる。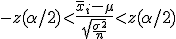

$-z( \alpha / 2) < \frac{ \bar{x}_i - \mu }{ \sqrt{ \frac{\sigma^2}{n} } } < z( \alpha / 2)$

区間推定では、調べたいのは母平均 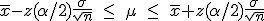$\normalsize \mu$ の範囲になるので、上の式を $\normalsize \mu$ について解くと、次の式が得られる。

$\bar{x} - z( \alpha / 2) \frac{ \sigma }{ \sqrt{n} } \hspace{5} \leq \hspace{5} \mu \hspace{5} \leq \hspace{5} \bar{x} + z( \alpha / 2) \frac{ \sigma }{ \sqrt{n} }$

▲ ▼

母分散が既知の場合

分散が $\normalsize \sigma^2$ 母集団から抽出した大きさ $\normalsize n$ の標本の平均（標本平均）が $\normalsize \bar{x}$ であるとき
母平均（母集団の平均） $\normalsize \mu$ の信頼度 100(1-α)% の信頼区間は次のとおり
$\bar{x} - z( \alpha / 2) \frac{ \sigma }{ \sqrt{n} } \hspace{5} \leq \hspace{5} \mu \hspace{5} \leq \hspace{5} \bar{x} + z( \alpha / 2) \frac{ \sigma }{ \sqrt{n} }$
- なお $\normalsize z$ は次のように標準化した統計量で、標準正規分布にしたがう
  $z = \frac{ \bar{x} - \mu }{ \frac{ \sigma }{ \sqrt{n} } }$
- 推定量（この場合は標本平均）の分散の平方根を標準誤差（SE : Standard Error）といい、次のように表す
  $SE = sqrt{ \frac{ \sigma^2 }{ n } } = \frac{ \sigma }{ \sqrt{n} }$
標本平均 $\normalsize \bar{x}$ の分布は正規分布にしたがい（中心極限定理より）、平均は $\normalsize \mu$ 、分散は $\normalsize \frac{ \sigma^2}{n}$ となる
標本数が多い場合にも使う

▲ ▼

母分散が未知の場合（t推定）

母標準偏差 $\normalsize \sigma$ のかわりに、標本標準偏差 $\normalsize s$ を用いる
- 分散は不偏分散になる
  $s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})$

母集団から抽出した大きさ $\normalsize n$ の標本の平均（標本平均）が $\normalsize \bar{x}$ 、分散（不偏分散） $\normalsize s^2$ がであるとき
母平均 $\normalsize \mu$ の信頼度 100(1-α)% の信頼区間は次のとおり
$\bar{x} - t(n-1, \alpha / 2) \frac{ s }{ \sqrt{n} } \hspace{5} \leq \hspace{5} \mu \hspace{5} \leq \hspace{5} \bar{x} + t(n-1, \alpha / 2) \frac{ s }{ \sqrt{n} }$
- $\normalsize t$ は次のように標準化した統計量で、t分布にしたがい、平均は $\normalsize \mu$ 、分散は $\normalsize \frac{ s^2}{n}$ となる
  $t = \frac{ \bar{x} - \mu }{ \frac{ s }{ \sqrt{n} } }$
- 標準誤差の推定値は $\normalsize \sqrt{ \frac{ s^2}{n} }$ となる
- $\normalsize t(n-1, \alpha / 2)$ は、自由度 n-1、確率α/2 のtの値
標本数が少ない場合にも用いる
- 自由度（すなわち標本数）が増えれば、t分布が標準正規分布 N(0, 1) に近づくので、母分散が既知の場合と同じになる