健康統計の基礎・健康統計学 - 2010/10th/Calculated_by_Standardization のバックアップ(No.2)
標準化を用いた確率の計算標準得点(標準正規分布の復習)平均が 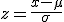 このときの 標準得点は、平均が0、分散が1の標準正規分布 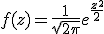 標準得点を使った確率の計算正規分布とみなされるデータを標準化すれば、 標準正規分布表を用いて、確率を計算することができます。 例題
つまり、「B大学の学生がAさんより身長が高い確率」は約80%(0.8)となる。 |
標準化を用いた確率の計算標準得点(標準正規分布の復習)平均が 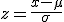 このときの 標準得点は、平均が0、分散が1の標準正規分布 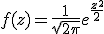 標準得点を使った確率の計算正規分布とみなされるデータを標準化すれば、 標準正規分布表を用いて、確率を計算することができます。 例題
つまり、「B大学の学生がAさんより身長が高い確率」は約80%(0.8)となる。 |