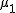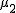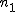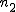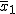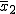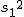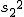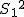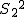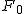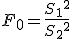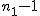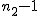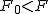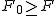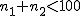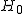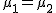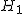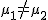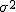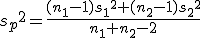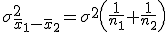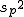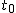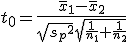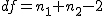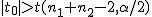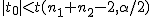[ ホーム | 一覧 | 検索 | 最終更新 | ヘルプ ] [ 新規 ]

健康統計の基礎・健康統計学 - 2009/12th/Unpaired_tTest のバックアップ(No.2)

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2009/12th/Unpaired_tTest へ行く。
- 1 (2009-07-07 (火) 05:41:55)
- 2 (2009-07-07 (火) 09:23:01)

対応のない2組の平均値の差の検定（母分散が未知だが等しい）

検定の対象

対応のない（独立した）2つの母集団について考える。それぞれの母数は次のとおり。ただし、母分散の値はわからない。

	母集団1	母集団2
母平均	$\normalsize \mu_1$	$\normalsize \mu_2$
標本の標本数	$\normalsize n_1$	$\normalsize n_2$
標本平均	$\normalsize \bar{x}_1$	$\normalsize \bar{x}_2$
標本分散	$\normalsize {s_1}^2$	$\normalsize {s_2}^2$

等分散の検定（F検定）

まず、未知の2組の母分散が等しいかどうかを調べる。

2組の標本の不偏分散について、次のようにあらわす
- 値の大きいほうの標本 : 不偏分散 $\normalsize {S_1}^2$ 、標本数 $\normalsize n_1$
- 値の小さいほうの標本 : 不偏分散 $\normalsize {S_2}^2$ 、標本数 $\normalsize n_2$
F分布にしたがう、等分散の検定の検定統計量 $\normalsize F_0$ を次の式から算出する
$F_0 = \frac{ {S_1}^2 }{ {S_2}^2 }$
- この式は、標本分散の比率から母分散の比率を推測することを意味している
第1自由度が $\normalsize n_1 -1$ 、第2自由度が $\normalsize n_2 - 1$ 、有意水準 $\normalsize \alpha$ の有意点 F の値と、検定統計量を比較する
- $\normalsize F_0 < F$ ならば、母分散は未知で「等しい」
  → t検定で調べる
- $\normalsize F_0 \geq F$ ならば、母分散は未知で「等しくない」
  → Welchの検定で調べる

t検定

標本数の和が $\normalsize n_1 + n_2 < 100$ の場合にも使われることがある

帰無仮説と対立仮説

対応のない（独立した）2組の母集団の平均に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の母集団の平均に差はない」 : $\normalsize \mu_1 = \mu_2$
対立仮説 $\normalsize H_{1}$ は「2組の母集団の平均に差がある」 : $\normalsize \mu_1 \neq \mu_2$

検定統計量の算出

標本分散から、全体の分散（母分散 $\normalsize \sigma^2$ の不偏推定量）を推測する
${s_p}^2 = \frac{(n_1 - 1){s_1}^2 + (n_2 - 1){s_2}^2}{ n_1 + n_2 -2 }$
標本平均の差の分散は、母分散を使って、次のように推測される
$\sigma_{ \bar{x}_1 - \bar{x}_2 }^2 = \sigma^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)$
母分散 $\normalsize \sigma^2$ を不偏推定量 $\normalsize {s_p}^2$ で代用し、t分布にしたがう、検定統計量 $\normalsize t_0$ を次の式から算出する
$t_0 = \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ {s_p}^2 } \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }$

仮説の判定（両側検定）

検定統計量 $\normalsize t_0$ と、自由度 $\normalsize df = n_1 + n_2 -2$ 、有意水準 $\normalsize \alpha$ の有意点の値（t分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |t_0| > t(n_1 + n_2 -2 , \alpha/2)$
  - 「有意に差がある」「検定の結果、有意である」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |t_0| < t(n_1 + n_2 -2 , \alpha/2)$
  - 「有意に差はない」「検定の結果、有意でない」「差があるとはいえない」

メニュー

授業内容

ケータイで教員にメール

mkawano%40ed.hyogo-dai.ac.jp

今日の5件

最新の10件

2025-06-02

2025-05-26

2025-05-19

2025/BHS/6th/1st

2025-05-12

total: 2745
today: 1
yesterday: 2
now: 4