健康統計の基礎・健康統計学 - 2025/BHS/11th/1st のバックアップ(No.1)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• 現在との差分 - Visual を表示
• ソース を表示
• 2025/BHS/11th/1st へ行く。
  • 1 (2025-06-30 (月) 18:35:53)

演習の内容

使用するファイルのダウンロード

今回の演習で使用するファイルを、 Moodleの授業のページからダウンロードして、 自分のパソコンに保存します。

1. Moodleにある授業のページにアクセスする
2. 「第11回」の「演習用ファイル（ダウンロードしてパソコンに保存）」をクリックする
3. 「名前を付けて保存」ボタンでファイルを保存した後、ファイルを開く

ダウンロードしたファイルを開いて、ウィンドウ上部の「編集を有効にする」をクリックして、演習をすすめます。

10.1 母平均の区間推定（148～153ページ）

信頼係数95%の信頼区間を求める（148～153ページ）

テキストの148～153ページまでの説明にしたがって、 信頼係数95%の母平均の区間推定をしますが、 次に指示をする箇所については、テキストの説明を読み替えて操作してください。

• 149ページ：手順１
  • あらかじめ入力済みなので、入力する必要はない
  • 次のようにして、COUNT関数を使って、E1セルにデータ数を計算

1. E1セルをクリックして選択
2. 「数式」タブの「関数の挿入」をクリック
3. 「関数の挿入」で、関数の分類に「統計」を選択し、「COUNT」を選択して「OK」をクリック
4. 「数値1」の欄に「B2:B9」を指定して「OK」をクリック

• 150ページ：手順３
  • E3セルに、STDEV.S関数を使って、B列の標本標準偏差を計算
• 151ページ：手順４
  • E5セルに、確率「0.05」を入力
  • E6セルに次の計算式を入力して、自由度（データ数-1）を計算

    =E1-1

  • E7セルに、T.INV.2T関数を使って、t分布の値（t値）を求める
    • 引数の「確率」の入力欄は「E5」セルを指定
    • 引数の「自由度」の入力欄は「E6」セルを指定
• 152ページ：手順５
  • E11セルに次の計算式を入力して、信頼区間の左側（下側信頼限界）を求める

    =E2-E7*E3/SQRT(E1)

• 153ページ：手順６
  • F11セルに次の計算式を入力して、信頼区間の右側（上側信頼限界）を求める

    =E2+E7*E3/SQRT(E1)

信頼区間を求められたら、D14セルに結論を文章で表現してください。
次のような表現になりますが、信頼区間の値（○○、△△）は小数点以下第2位までで、第3位を四捨五入してください。

時給の母平均は○○から△△の間に含まれる

信頼係数99%の信頼区間を求める

信頼係数95%の信頼区間の求め方を参考に、 次のセルに計算をして、 信頼係数99%の母平均の区間推定を求めてください。

• I5セル：「0.01」と入力
• I6セル：自由度を計算
• I7セル：T.INV.2T関数を使って、t分布の値（t値）を計算
• I11セル：信頼区間の左側（下側信頼限界）を計算
• I12セル：信頼区間の右側（上側信頼限界）を計算

信頼区間を求められたら、95%信頼区間と同じように、 H14セルに結論を文章で表現してください。
信頼区間の値は小数点以下第2位までで、第3位を四捨五入してください。

シートの切り替え

ここまでの演習ができたら、 使用するシート（ワークシート）を切り替えてください。

1. ウィンドウ左下の「10.2」をクリック
2. 表示されるシートが切り替わる

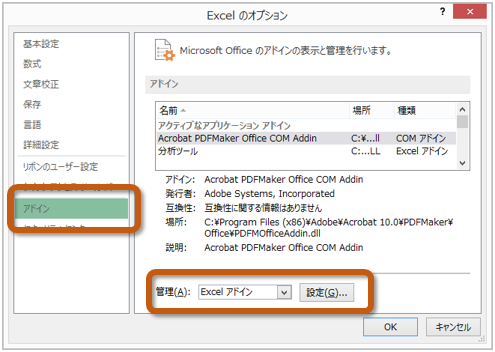
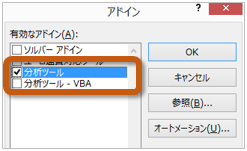
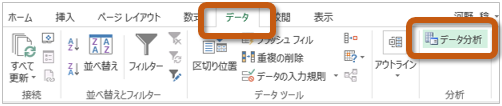
10.2 分析ツールの利用法（154～155ページ）

まず、次のように操作して、分析ツールを読み込みます。

1. 「ファイル」タブをクリック（古いOfficeの場合は、「Office」ボタンをクリック）
   
2. 左側のメニューから「オプション」を選択
   
3. 「Excelのオプション」ウィンドウの左側から「アドイン」を選択し、 「管理(A)」を「Excelアドイン」に設定した後、「設定」ボタンをクリック
   
4. 「アドイン」ウィンドウの「分析ツール」をクリックしてチェックをしたら、「OK」ボタンをクリック
   
5. 分析ツールを使うときは、「データ」タブにある「分析ツール」をクリック
   

分析ツールを読み込めたら、 テキストの154～155ページまでの操作をして、 基本統計量を求めて、 テキスト155ページの結果と一致するかを確かめてください。

シートの切り替え

ここまでの演習ができたら、 使用するシート（ワークシート）を切り替えてください。

1. ウィンドウ左下の「11.1」をクリック
2. 表示されるシートが切り替わる

11.1 母比率の区間推定（156～161ページ）

信頼係数95%の信頼区間を求める（156～161ページ）

テキストの156～161ページまでの説明にしたがって、 信頼係数95%の母比率の区間推定をしますが、 次に指示をする箇所については、テキストの説明を読み替えて操作してください。

• 158ページ：手順１
  • あらかじめ入力済みなので、入力する必要はない
• 159ページ：手順３
  • B6セルに、確率「0.05」を入力
  • B7セルに、NORM.INV関数を使って、標準正規分布の値（z値）を求める
    • 引数の「確率」の入力欄は「1-B6/2」と入力（0.975と計算したことになる）
    • 引数の「平均」の入力欄は「0」と入力
    • 引数の「標準偏差」の入力欄は「1」と入力
• 160ページ：手順４
  • B11セルに次の計算式を入力して、信頼区間の左側（下側信頼限界）を求める

    =B4-B7*SQRT(B4*(1-B4)/C2)

• 161ページ：手順５
  • C11セルに次の計算式を入力して、信頼区間の右側（上側信頼限界）を求める

    =B4+B7*SQRT(B4*(1-B4)/C2)

信頼区間を求められたら、A14セルに結論を文章で表現してください。
次のような表現になりますが、信頼区間の値（○○、△△）は小数点以下第2位までで、第3位を四捨五入してください。

生息比率は○○から△△の間に含まれる

信頼係数99%の信頼区間を求める

信頼係数95%の信頼区間の求め方を参考に、 次のセルに計算をして、 信頼係数99%の母比率の区間推定を求めてください。

• F6セル：「0.01」と入力
• F7セル：NORM.INV関数を使って、標準正規分布の値（z値）を計算
• F11セル：信頼区間の左側（下側信頼限界）を計算
• G12セル：信頼区間の右側（上側信頼限界）を計算

信頼区間を求められたら、95%信頼区間と同じように、 E14セルに結論を文章で表現してください。
信頼区間の値は小数点以下第2位までで、第3位を四捨五入してください。