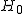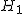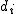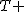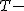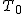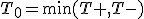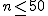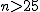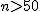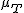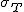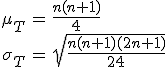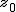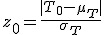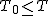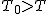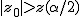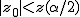[ ホーム | 一覧 | 検索 | 最終更新 | ヘルプ ] [ 新規 ]

健康統計の基礎・健康統計学 - 2009/14th/ANOVA のバックアップ(No.1)

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2009/14th/ANOVA へ行く。
- 1 (2009-07-22 (水) 07:21:50)
- 2 (2009-07-22 (水) 09:48:43)
- 3 (2009-07-22 (水) 10:50:06)
- 4 (2009-07-23 (木) 02:09:32)

一元配置分散分析

平均値の差の検定で、3つ以上の標本について平均値の差を比較するときに使用する
- 2つの標本の平均値の差の検定は「[[（対応のない）t検定>../../12th/Unpaired_tTest ]]」を使う
- もし、3つ以上の標本についてt検定を使う（2組ずつのペアで検定をする）と、例えば差がないにもかかわらず差があると検定してしまう危険性がある
分散分析（ANOVA : ANalysis Of VAriance）は、標本同士の平均値の差の程度がそれぞれの標本内の誤差に比べて大きいかを調べて分析する方法である

検定の対象

因子と水準

対応のない複数の組の標本について考える。

例えば、3つの血圧降下剤（A薬、B薬、C薬）の効果を調べるために、 15人の被験者を無作為に3つのグループに分けて、それぞれのグループにA薬、B薬、C薬いずれかを投与して収縮期血圧を測定したところ、次の表のようになったとする。

番号	A薬	B薬	C薬	全体
1	116	106	108
2	128	102	100
3	129	108	108
4	137	118	114
5	140	116	110
合計	650	550	540	1740
平均	130	110	108	116

差を調べる変数の要因を「因子」という
- 上の表では「血圧」にあたる
- ひとつの因子について分析することから「一元配置分散分析」という
要因の内容が異なるグループを「水準」という
- 上の表では「A薬、B薬、C薬」のような項目にあたる
各水準の標本数（データの個数）を「繰り返し数」という

一般には、一元配置分散分析のデータは、次のような表で書くことができる。

番号	1	2	…	\mimetex(\normalsize p );	全体
1	\mimetex(\normalsize x_{11} );	\mimetex(\normalsize x_{21} );	…	\mimetex(\normalsize x_{p1} );
2	\mimetex(\normalsize x_{12} );	\mimetex(\normalsize x_{22} );	…	\mimetex(\normalsize x_{p2} );
…
	\mimetex(\normalsize x_{1 {n_1} } );	\mimetex(\normalsize x_{2 {n_2} } );	…	\mimetex(\normalsize x_{p {n_p} } );
繰り返し数	\mimetex(\normalsize n_1 );	\mimetex(\normalsize n_2 );	…	\mimetex(\normalsize n_p );	\mimetex(\normalsize n );
平均	\mimetex(\normalsize \bar{ x_1 } );	\mimetex(\normalsize \bar{ x_2 } );	…	\mimetex(\normalsize \bar{ x_p } );	\mimetex(\normalsize \bar{x} );

	1	2	3	4	5	6	7	8	9	10
標本A	269	230	365	282	295	212	346	207	308	257
標本B	273	213	383	282	297	213	351	208	294	238
差 d	-4	17	18	0	-2	-1	-5	-1	14	19
順位	4	7	8		3	1.5	55	1.5	6	9

ウィルコクソンの符号付順位検定

データ対の順位がわかる場合は、符号検定よりも効率が良い

帰無仮説と対立仮説

対応のある2組の標本の代表値に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の標本の代表値に差はない」
対立仮説 $\normalsize H_{1}$ は「2組の標本の代表値に差がある」

検定統計量の算出

2つの標本の差 $\normalsize d_i$ の順位の和を、次のように求める
- 差 $\normalsize d_i$ が正の値の順位の和を $\normalsize T+$ とする
- 差 $\normalsize d_i$ が負の値の順位の和を $\normalsize T-$ とする
$\normalsize T+$ と $\normalsize T-$ の小さい方の値を $\normalsize T_0$ とする。
- 標本数 $\normalsize n$ は、差が0でない組の数とする
  $T_0 = \min ( T+ , T-)$

$\normalsize n \leq 25$ （または $\normalsize n \leq 50$ ）の場合…
- ウィルコクソンの符号付順位検定表から、標本数 $\normalsize n$ に対応する $\normalsize T$ の値を求める

$\normalsize n > 25$ （または $\normalsize n > 50$ ）の場合…
- 平均 $\normalsize \mu_{T}$ と標準偏差 $\normalsize \sigma_{T}$ を次の式から求める
  $\begin{eqnarray}\mu_{T} &=& \frac{n(n+1)}{4} \\\sigma_{T} &=& \sqrt{ \frac{ n(n+1)(2n+1) }{24} }\end{eqnarray}$
- 標準正規分布にしたがう、検定統計量 $\normalsize z_0$ を次の式から算出する
  $z_0 = \frac{ | T_0 - \mu_{T} | }{ \sigma_{T} }$

仮説の判定（検定表からの算出）

$\normalsize n \leq 25$ （または $\normalsize n \leq 50$ ）の場合…
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize T_0 \leq T$
  - 「有意に差がある」「検定の結果、有意である」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize T_0 > T$
  - 「有意に差はない」「検定の結果、有意でない」「差があるとはいえない」

$\normalsize n > 25$ （または $\normalsize n > 50$ ）の場合…
検定統計量 $\normalsize z_0$ と、有意水準 $\normalsize \alpha$ の有意点の値（標準正規分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |z_0| > z(\alpha/2)$
  - 「有意に差がある」「検定の結果、有意である」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |z_0| < z(\alpha/2)$
  - 「有意に差はない」「検定の結果、有意でない」「差があるとはいえない」

メニュー

授業内容

ケータイで教員にメール

mkawano%40ed.hyogo-dai.ac.jp

今日の5件

最新の10件

2025-06-02

2025-05-26

2025-05-19

2025/BHS/6th/1st

2025-05-12

total: 17331
today: 1
yesterday: 3
now: 3