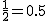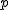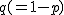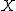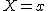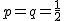仮説検定の考え方仮説検定の考え方について、簡単な例を用いて考えてみましょう。 コインを投げて表が出た回数を数える例として、コインを10回投げて、表が出た回数を数えることを考えてみましょう。 ゆがみがない、いわゆる「かたよりのない」コインであれば、
コインを1回投げた結果、表が出る確率も裏が出る確率も、
ちょうど半分の そこで、「あるコイン」を10回投げたところ、 表が9回も出たとします。 この「あるコイン」は「かたよりがない」コインでしょうか? それとも「かたよりがある」コインでしょうか? 「コインにはかたよりがない」という仮説を立てる仮説検定では、母集団に対するある仮説を立てます。 そして、母集団から取り出した一部分、つまり標本を使って、 その結果が偶然のものなのか必然なのかを確率的に調べて、 仮説が正しいかどうかを判断する方法です。 今、「コインを10回投げたうち9回表がでた」ことについて考えています。 コインにかたよりがある可能性がありそうです。 そのことを仮説検定で確かめてみましょう。 仮説検定では、どちらかというと主張したいことに反対の仮説をまず考えます。 これが、「母集団に対するある仮説」になります。 この仮説を「無に帰することを予定した」という意味で、 「帰無仮説」といいます。 そして、帰無仮説に対立する仮説、つまり、 どちらかといえば主張したい仮説を「対立仮説」といいます。 もしコインにかたよりがあるとしても、どの程度かたよっているかまではわかりません。 そこで、帰無仮説として「コインにかたよりはない」という仮説を立てることにします。 まとめると、帰無仮説と対立仮説は次のようになります。
コインの表が出る回数の確率を求める次に、帰無仮説として立てた仮説のもとでの確率を求めて、 その確率をもとに、 今考えている事象(コインを10回投げたら9回表が出た)が偶然起こったことか 必然的に起こったことかを判断してみましょう。 コインのように表または裏の2種類の結果を考えるには、
第9回で学習した、二項分布の考え方を利用します。
二項分布は、ある独立な試行について事象 ![\begin{eqnarray}\mathrm{P}( X=x ) &=& {_n} \mathrm{C}_x p^x q^{n-x} \\[10]&=& \frac{n!}{x! (n-x)!} p^x q^{n-x} \\[10]&=& \frac{n!}{x! (n-x)!} p^x (1-p)^{n-x}\end{eqnarray}](cache/20bbcdc83e5cab12cbc397d3c4f214d3.mimetex.gif) 今回は、10回のうち表がでる回数を確率変数 ![\begin{eqnarray}\mathrm{P}( X=x ) &=& { _{10} } \mathrm{C}_x \left(\frac{1}{2}\right)^x \left(\frac{1}{2}\right)^{10-x} \\[10]&=& {_{10} } \mathrm{C}_x \left(\frac{1}{2}\right)^{10} \\[10]&=& \frac{ {_{10} } \mathrm{C}_x }{1024}\end{eqnarray}](cache/30053cf26f77914ca72232fe5cbae133.mimetex.gif) この式を計算した結果を、確率分布として次のようにまとめておきます。
仮説から求めた確率をもとに判断でする今考えている仮説は「コインはかたよりがない」です。 では、10回中9回表が出るコインにかたよりがないのかあるのかを判断するには、 どうすればよいでしょう。 ここで、「コインにかたよりがないという仮説のもとで、 まれなこと(ある一定の確率以下の出来事)が起きた場合は、 そのコインはかたよりがないとは見なせない」としましょう。 これが仮説検定では重要な考え方です。 この「まれなこと」が起きたと判断する基準を、 有意水準といいます。 有意水準はあらかじめ決めておきます。 一般には5%(0.05)か1%(0.01)が使われます。 今回は有意水準を5%としておきましょう。
表が9回はでる確率は、「表が9回でた」場合と「表が10回でた」場合の確率を足し合わせたものになります。少なくとも9回は出た、と考えます。 確率分布の表から、表が9回は出る確率は、0.010+0.001=0.011となります。 有意水準を5%(0.05)と考えると、それより小さい確率です。 有意水準より小さい確率で起きてしまったことを、 仮説検定では「仮説では起こるはずのないことが起こった」と見なします。 このことを「帰無仮説を棄却する」といいます。 もし、有意水準より大きい確率だった場合は、 「仮説で起こるはずのないことが起こらなかった」とみなして、 「帰無仮説を棄却できなかった」といいます。 今回の場合、表が9回でるのはめったに起こらないことが起こったので、 帰無仮説を棄却し、「コインにはかたよりがある」という判断になります。 ちなみに、表が8回でたコインが別にあったとしましょう。 そのコインにかたよりがあるかどうかを考えると、 8回以上表が出る確率は、確率分布から求めると、 0.044+0.010+0.001=0.055となり、有意水準5%を超えることになります。 つまり「コインにかたよりがないとはいえない」という判断になります。 |