点推定と区間推定
点推定(point estimation)
点推定とは
- 標本の特性値1つから母集団の特性値を推定する
- 母数(パラメータ):母集団の特性値(統計量)
- 母平均(母集団の平均)、母分散(母集団の分散)、母比率(母集団の比率)
- 直接調べることはできない
- 推定量:標本をもとに母数として推定した統計量
- 標本平均(標本の平均)、不偏分散(標本の分散)、標本比率(標本の比率)
- 推定値:推定量から求めた具体的な値
- 点推定では、標本の推定値が必ずしも母数と一致するとは限らない(たいてい誤差が生じる)
推定量の望ましい性質
- 不偏性
- その期待値(平均値)が母数と一致する推定量を「不偏推定量」という
- 標本平均について、その期待値は母平均に一致する(中心極限定理へ)
- 一致性
- 標本数を大きくしていくと推定値が母数に近づく推定量を「一致推定量」という
- 大数の法則から明らか(統計的確率は数学的確率に近づく)
- 有効性
- ある母数に対して2つ以上の推定量がある場合に分散(誤差)の小さい推定量を「有効推定量」という
- 標本の中央値に比べ、標本平均の方が、分布の分散が小さい
区間推定(interval estimation)
区間推定とは
- 標本の推定量から、「ある確率」で、母集団の特性値(母数)の範囲を示す
信頼区間と信頼係数
- 信頼区間
- 「ある」確からしさで示される、母集団の特性値の範囲
- 95%信頼区間
- 標本から平均値を出したとき、母平均(母集団の平均)がその区間にあるのが100回中95回以上の確率で、間違える危険性が5回未満
- 99%信頼区間
- 標本から平均値を出したとき、母平均(母集団の平均)がその区間にあるのが100回中99回以上の確率で、間違える危険性が1回未満
- 注意:「母平均の値が95(または99)%の確率でその区間のどこかにある」と解釈してはいけない
- 信頼限界:信頼区間の上限および下限の値
- 信頼係数
- 区間推定の確実性をあらわし、「1-α」(αは0.05または0.01)であらわす
- 信頼度 : 100×(1-α) %
区間推定の考え方
- 標本の推定量(標本平均、標本比率など)の分布を選択する
- 推定量の分布の平均と分散(標準偏差)を求める
- 母数にあった方法で、信頼区間を算出する
- 一般的には次のようになる
- 信頼下限:<推定量>−<分布における確率αの値>×<推定量の標準偏差(標準誤差)>
- 信頼上限:<推定量>+<分布における確率αの値>×<推定量の標準偏差(標準誤差)>
中心極限定理(central limit theorem)
- 平均が
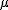 、分散が 、分散が 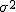 の母集団から大きさ の母集団から大きさ  の標本を抽出して、その標本平均 の標本を抽出して、その標本平均 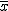 を調べると、その分布は平均が を調べると、その分布は平均が 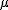 、分散が 、分散が 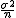 の正規分布に従う( の正規分布に従う( は十分大きな数とする) は十分大きな数とする)
|
|