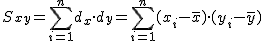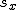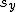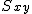2009/4th/Correlation のバックアップ(No.3) - 健康統計の基礎・健康統計学

バックアップ一覧
差分を表示
現在との差分を表示
現在との差分 - Visual を表示
ソースを表示
2009/4th/Correlation へ行く。
- 1 (2009-04-23 (木) 13:10:35)
- 2 (2009-04-28 (火) 07:05:16)
- 3 (2009-04-29 (水) 03:23:40)
- 4 (2009-04-29 (水) 04:38:39)
- 5 (2009-04-29 (水) 06:20:42)
- 6 (2009-05-01 (金) 02:28:40)

相関 (correlation)

2種類のデータのあいだになんらかの関係がある場合、統計学的な関係がみられるときに、「相関がある」という。

データの大小に関して、一方の値が変わるにつれて、もう一方の値も変わる
- 身長と体重
- 収縮期血圧と拡張期血圧

▲ ▼

相関係数 (correlation coefficient)

▲ ▼

相関の種類

線形相関：相関（関係）を示すグラフが1本の直線で近似できる
- 順相関：相関が正の場合（グラフが右肩あがりの直線）
- 逆相関：相関が負の場合（グラフが右肩さがりの直線）
非線形相関：相関を示すグラフが指数関数や2次・3時間数のように直線状をしていない

▲ ▼

相関係数

相関係数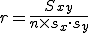とは、相関の程度をあらわす
相関係数 $\normalsize r$ は、次の値をとる。
$-1 \leq r_s \leq +1$
- 完全相関：相関係数が±1の場合
- 無相関：相関係数が0の場合

相関係数 $\normalsize r$ は、次のような式で求められる

$r=\frac{ S_{xy} }{n \times s_x \cdot s_y}$

偏差積和（偏差の積の合計）
$\normalsize\displaystyle S_{xy} = \sum_{i=1}^n d_x \cdot d_y = \sum_{i=1}^n (x_i - \bar{x})\cdot(y_i - \bar{y})$
標本数: $\normalsize n$
標準偏差: $\normalsize s_x$ , $\normalsize s_y$

▲ ▼

偏差積和

偏差積和（偏差の積和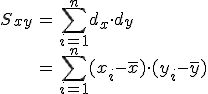） $\normalsize S_{xy}$ とは、偏差（各データと平均の差）の積の総和である。

$\begin{eqnarray}S_{xy} &=& \sum_{i=1}^n d_x \cdot d_y \\&=& \sum_{i=1}^n (x_i - \bar{x})\cdot(y_i - \bar{y})\end{eqnarray}$

標本数: $\normalsize n$

▲ ▼

共分散

共分散 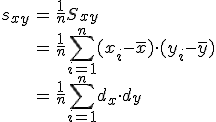$\normalsize s_{xy}$ は、偏差積和を標本数で割ったもの。

$\begin{eqnarray}s_{xy} &=& \frac{1}{n} S_{xy} \\&=& \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})\cdot(y_i - \bar{y}) \\&=& \frac{1}{n} \sum_{i=1}^n d_x \cdot d_y\end{eqnarray}$

標本数: $\normalsize n$

▲ ▼

相関関係と因果関係

▲ ▼

相関関係から因果関係を確定するときの注意点

関連の時間性
- 原因は結果の前にあるか
関連の密接性
- 原因が結果に密接に関連するか
関連の特異性
- 原因が結果のは性にどの程度かかわっているか
関連の普遍性
- 対象や時期、方法などが異なっていても、類似した結果が得られるか
関連の合理性
- 従来の理論や経験から考えて矛盾がないか

疑似相関: 直接の相関はないが何かある要因が2つの事象と相関しているために、 2つの事象に相関がみられるケースがある。

▲ ▼

相関の程度

相関係数の値から、相関の程度を次のように記述できる。

-1.0≦相関係数r<-0.7	強い負の相関
-0.7≦相関係数r<-0.4	かなりな負の相関
-0.4≦相関係数r<-0.2	やや負の相関
-0.2≦相関係数r≦0.2	ほとんど相関がない
0.2<相関係数r≦0.4	やや正の相関
0.4<相関係数r≦0.7	なかりな正の相関
0.7<相関係数r≦1	強い正の相関

なお、標本数が少ない場合は、母相関係数の推定や検定（後日説明）が必要となる。

▲ ▼

順位相関係数

スピアマン（Spearman）の順位相関係数 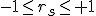$\normalsize r_s$ は、相関係数と同様、次の値をとる。

$-1 \leq r_s \leq +1$

メニュー

授業内容

ケータイで教員にメール

健康統計の基礎・健康統計学 - 2009/4th/Correlation のバックアップ(No.3)