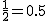2010/13th/Hypothesis_Testing_Approach のバックアップ(No.1)

仮説検定の考え方

仮説検定の考え方について、簡単な例を用いて考えてみましょう。

例として、コインを10回投げて、表が出た回数を数えることを考えてみましょう。

ゆがみがない、いわゆる「かたよりのない」コインであれば、コインを1回投げた結果、表が出る確率も裏が出る確率も、ちょうど半分の $\normalsize \frac{1}{2} = 0.5$ と考えて問題ないでしょう。つまり、10回投げた結果として表が出る回数は5回ぐらいが最も多いと考えられます。

そこで、「あるコイン」を10回投げたところ、表が9回も出たとします。この「あるコイン」は「かたよりがない」コインでしょうか？それとも「かたよりがある」コインでしょうか？

仮説検定では、母集団に対するある仮説を立てます。そして、母集団から取り出した一部分、つまり標本を使って、その結果が偶然のものなのか必然なのかを確率的に調べて、仮説が正しいかどうかを判断する方法です。

今、「コインを10回投げたうち9回表がでた」ことについて考えています。コインにかたよりがある可能性がありそうです。そのことを仮説検定で確かめてみましょう。

仮説検定では、どちらかというと主張したいことに反対の仮説をまず考えます。これが、「母集団に対するある仮説」になります。