順列と組み合わせ

ある数 n から１ずつ少ない数を掛けあわせることを「階乗」という
$\begin{eqnarray}n! &=& n \times (n - 1) \times (n - 2) \times \cdots \times 2 \times 1\end{eqnarray}$

異なる n 個のものから r 個を選んだ「並べ方」を、 n 個から r 個をとる「順列」という
$\begin{eqnarray}_n \mathrm{P}_r &=& n \times (n - 1) \times (n - 2) \times \cdots \times (n - r + 1) \\[10]&=& \frac{ n! }{ (n-r)! }\end{eqnarray}$
n 個から n 個をとる順列
$\begin{eqnarray}_n \mathrm{P}_n &=& n \times (n - 1) \times (n - 2) \times \cdots \times 2 \times 1 = n!\end{eqnarray}$
7 個から 3 個をとる順列
$\begin{eqnarray}_7 \mathrm{P}_3 &=& 7 \times 6 \times 5 = 210\end{eqnarray}$

また次のようなことがいえる（n 個から0個をとる順列）
$\begin{eqnarray}_n \mathrm{P}_0 &=& 0\end{eqnarray}$

異なる n 個のものから r 個を選ぶときの組み合わせを、 n 個から r 個をとる「組み合わせ」という
$\begin{eqnarray}_n \mathrm{C}_r &=& \frac{ _n \mathrm{P} _r }{ r! } \\[10]&=& \frac{ n \times (n - 1) \times \cdots \times (n - r + 1) }{ r! } \\[10]&=& \frac{ n! }{ r! (n-r)! }\end{eqnarray}$
4 個から 3 個をとる組み合わせ
$\begin{eqnarray}_4 \mathrm{C}_3 &=& \frac{ 4 \times 3 \times 2 }{ 1 \times 2 \times 3 } = 4\end{eqnarray}$
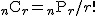なぜ $\normalsize {}_n \mathrm{C}_r = {}_n \mathrm{P}_r / r!$ となるか？
- {a, b, c, d, e} の5つから {a, b, c} の3つを選ぶ場合を考えると…
  - 順列は次の 3!=6 通りとなる
    {a,b,c}, {a,c,b}, {b,a,c}, {b,c,a}, {c,a,b}, {c,b,a}
  - 組み合わせでは順序を考えないので、順列の結果を選び出した3つの場合の数 3!=6 で割ってやればよい

また次のようなことがいえる
$\begin{eqnarray}_n \mathrm{C}_0 &=& 1 \\[10]_n \mathrm{C}_1 &=& n \\[10]_n \mathrm{C}_n &=& 1 \\[10]_n \mathrm{C}_r &=& _n \mathrm{C}_{n-r}\end{eqnarray}$

健康統計の基礎・健康統計学 - 順列と組み合わせ