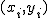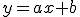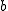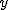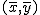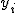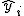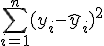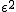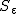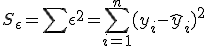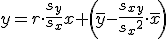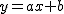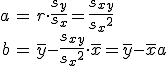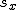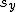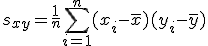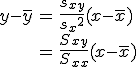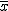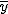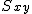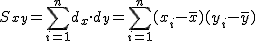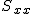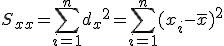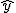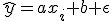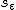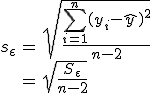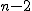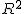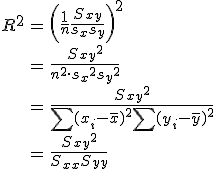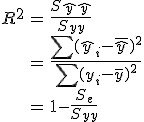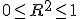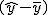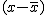Top > 2014 > 5th > Regression
AND OR

回帰 (regression)

データをもとに、ある変数（従属変数または目的変数）を 別の変数（独立変数または説明変数）で 予測する式を作るための統計的手法を、 「回帰分析」（regression analysis）といいます。

とくに、独立変数が1つだけの場合を単回帰分析といいます。 複数の独立変数で1つの従属変数を予測する場合は重回帰分析といいます。

▲ ▼

回帰直線 (regression line)

▲ ▼

回帰直線

  • 散布図の各点 \normalsize (x_i, y_i) が近くに分布するような直線を回帰直線という。
    y = ax + b
    • 回帰係数（回帰直線の傾き）：\normalsize a
    • 回帰直線のy切片（x=0 のときのyの値）：\normalsize b
    • 独立変数（説明変数：予測に使う変数）：\normalsize x
    • 従属変数（目的変数、基準変数：予測したい変数）：\normalsize y
  • なお、回帰式は必ず \normalsize (\bar{x}, \bar{y}) を通る
▲ ▼

最小二乗法（least squares method）

  • 観測値（または実測値） \normalsize y_i と 推定値（または予測値） \normalsize \hat{y}_i との差（残差 \normalsize \epsilon ）の2乗の和が最小になるような \normalsize a と \normalsize b を求める。
    • 次の値が最小となるような、\normalsize a と \normalsize b を求める。
      \sum_{i=1}^n (y_i - \hat{y}_i)^2
    • 残差の二乗 \normalsize \epsilon^2 を足したものを、残差平方和 \normalsize S_{\epsilon} という
      S_{\epsilon} = \sum \epsilon^2 = \sum_{i=1}^n (y_i - \hat{y}_i)^2
▲ ▼

回帰式の計算

  • \normalsize x を独立変数（横軸）、 \normalsize y を従属変数（縦軸）としたときの回帰式 （ \normalsize y への \normalsize x からの回帰式）は 次のようになる。
    y = r \cdot \frac{s_y}{s_x} x + \left( \bar{y} - \frac{s_{xy} }{ {s_x}^2 } \cdot \bar{x} \right)
    • なお、回帰式を \normalsize y = ax + b とすると、 \normalsize a と \normalsize b は次のようになる。
      \begin{eqnarray}a &=& r \cdot \frac{s_y}{s_x} = \frac{s_{xy} }{ {s_x}^2 } \\b &=& \bar{y} - \frac{s_{xy} }{ {s_x}^2 } \cdot \bar{x} = \bar{y} - \bar{x} a\end{eqnarray}
    • 相関係数: \normalsize r
    • 2変数の標準偏差: \normalsize s_x , \normalsize s_y
    • 2変数の共分散（偏差積和の平均）
      s_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})
  • 回帰式を変形すると、次のようになる。
    \begin{eqnarray}y - \bar{y} &=& \frac{s_{xy} }{ {s_x}^2 } (x - \bar{x}) \\&=& \frac{ S_{xy} }{ S_{xx} } (x - \bar{x})\end{eqnarray}
    • 2変数の平均値: \normalsize \bar{x} , \normalsize \bar{y}
    • 2変数の偏差積和：\normalsize S_{xy}
      \normalsize\displaystyle S_{xy} = \sum_{i=1}^n d_x \cdot d_y = \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y})
    • 偏差平方和：\normalsize S_{xx}
      S_{xx} = \sum_{i=1}^n {d_x}^2 = \sum_{i=1}^n (x_i - \bar{x})^2
▲ ▼

標準誤差（standard error）

  • 予測値と実測値のずれ（予測値 \normalsize \hat{y} との誤差；残差 \normalsize \epsilon ）について考える
    \hat{y} = a x_i + b + \epsilon
  • 残差の標準偏差を、標準誤差 \normalsize s_{\epsilon} という
    \begin{eqnarray}s_{\epsilon} &=& \sqrt{ \frac{ \sum_{i=1}^{n} (y_i - \hat{y})^2 }{ n-2 } } \\&=& \sqrt{ \frac{ S_{\epsilon} }{ n-2 }\end{eqnarray}
    • \normalsize n-2 で割っているのは、2つの係数を推定したことによる自由度（後日説明）の修正のため
▲ ▼

決定係数（coefficient of determination）

  • 相関係数の二乗を決定係数（または寄与率）\normalsize R^2 という。
    \begin{eqnarray}R^2 &=& \left( \frac{1}{n} \frac{ S_{xy} }{s_x s_y} \right)^2 \\&=& \frac{ { S_{xy} }^2 }{n^2 \cdot { s_{x} }^2 { s_{y} }^2 } \\&=& \frac{ { S_{xy} }^2 }{ \sum (x_i - \bar{x} )^2 \sum (y_i - \bar{y} )^2 } \\&=& \frac{ { S_{xy} }^2 }{S_{xx} S_{yy} }\end{eqnarray}
  • 偏差平方和と残差平方和を使うと、次のように書くこともできる
    \begin{eqnarray}R^2 &=& \frac{ S_{ \hat{y}\hat{y} } }{ S_{yy} } \\&=& \frac{ \sum (\hat{y}_i - \bar{ \hat{y} } )^2 }{ \sum (y_i - \bar{y} )^2 } \\&=& 1 - \frac{ S_e }{ S_{yy} }\end{eqnarray}
  • 決定係数は、0から1の値をとる。
    0 \leq R^2 \leq 1
  • 推定（回帰式）の精度を表す指標である
    • 「従属変数 \normalsize y の分散の何％を予測値 \normalsize \hat{y} の分散が説明しているか」を示す
      • 別の言い方をすると、「説明変数が従属変数の何％にあたる部分に影響を与えているか（寄与しているか）」を示す
    • だいたい、0.5以上であれば精度が高いといえる
▲ ▼

回帰の概念

  • 予測値 \normalsize \hat{y} と従属変数の平均 \normalsize \bar{y} との差は、一般に独立変数 \normalsize x とその平均 \normalsize \bar{x} との差より小さくなる
    • →予測値と平均の差 \normalsize ( \hat{y} - \bar{y}) との差は、独立変数と平均の差 \normalsize (x - \bar{x}) との差より小さくなる
    • →予測値は独立変数に比べて平均に近づく
  • 統計学的な現象で、「回帰効果」や「平均への回帰」ともいう
    • （例）1回目の試験の結果が偏っていた（とくに良い、悪いなど）人について、2回目の試験結果を調べると、その平均値は1回目の結果よりも1回目の全体の平均値に近くなる（時間的には逆で考えてもよい）
    • （例）父親と子どもの身長を比較して、とくに身長の高い父親でも、とくに身長の低い父親からでも、子どもたちの身長は父親たちの身長より平均に近くなる
    • （例）とくに身長の高い人たちの父親の身長は、子どもたちの身長よりも平均に近い（全体の身長の分布は、父親たちも子どもたちも同じ）
リロード   差分   ホーム 一覧 検索 最終更新 バックアップ リンク元   ヘルプ   最終更新のRSS
Last-modified: Wed, 14 May 2014 18:51:04 JST (3627d)