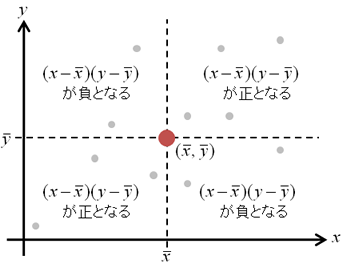
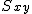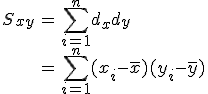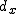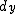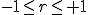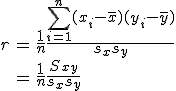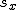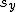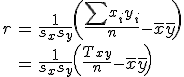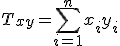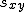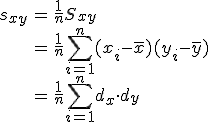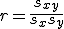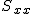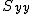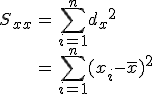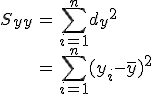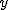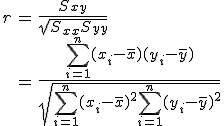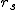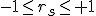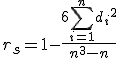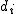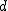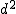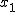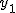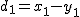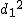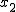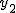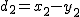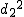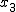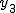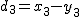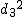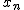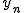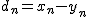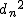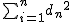相関 - 健康統計の基礎・健康統計学

[ ホーム | 一覧 | 検索 | 最終更新 | ヘルプ ] [ 新規 | 編集 | 添付 ]

Top > 2013 > 6th > Correlation

相関 (correlation)

2種類のデータの間に何らかの関係がある場合、統計学的な関係性がみられるときに、「相関がある」や「相関関係がある」といいます。

データの大小に関して、一方の値が変わるにつれて、もう一方の値も変わる
- 身長と体重
- 収縮期血圧と拡張期血圧

データの尺度と相関関係

データを大雑把に、量的データ（比例尺度、間隔尺度）と質的データ（順序尺度、名義尺度）に分けるときに、データの尺度によって、相関関係を表す指標は異なります。次の表を参考にしてください。

2つのデータの尺度	相関関係を表す指標
量的データ×量的データ	ピアソンの積率相関係数
順位データ×順位データ	スピアマンの順位相関係数
量的データ×質的データ	相関比
質的データ×質的データ	クラメールの連関（関連）係数

この授業では、よく利用される、ピアソンの積率相関係数とスピアマンの順位相関係数を扱います。

相関係数 (correlation coefficient)

相関の種類

線形相関：相関（関係）を示すグラフ（散布図）が1本の直線で近似できる
- 順相関：相関が正の場合（散布図が右肩あがりの傾向）
- 逆相関：相関が負の場合（散布図が右肩さがりの傾向）
- 無相関：相関がない場合（散布図がまばらになっている）
非線形相関：相関を示すグラフが指数関数や2次・3次関数のように曲線状になる

偏差積和

偏差積和（偏差の積の総和） $\normalsize S_{xy}$ とは、偏差（各データと平均の差）の積の総和である。
$\begin{eqnarray}S_{xy} &=& \sum_{i=1}^n d_x d_y \\&=& \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y})\end{eqnarray}$
- 標本数: $\normalsize n$
- 偏差: $\normalsize d_x$ , $\normalsize d_y$
偏差の積とデータの分布は次のようなイメージになる

相関係数（ピアソンの積率相関係数）

相関係数（ピアソン(Pearson)の積率相関係数） $\normalsize r$ は、相関の程度をあらわし、次の値をとる。
（一般に相関係数といえばコレ）
$-1 \leq r \leq +1$
- 完全相関：相関係数がちょうど±1の場合
- 無相関：相関係数が0の場合

相関係数 $\normalsize r$ は、次の式で求められる
$\begin{eqnarray}r &=& \frac{1}{n} \frac{ \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y}) }{s_x s_y} \\&=& \frac{1}{n} \frac{ S_{xy} }{s_x s_y}\end{eqnarray}$
- 標本数: $\normalsize n$
- 標準偏差: $\normalsize s_x$ , $\normalsize s_y$
- 偏差積和: $\normalsize S_{xy}$

または、次の式でも求められる（統計量だけから計算できる）
$\begin{eqnarray}r &=& \frac{ 1 }{s_x s_y} \left( \frac{ \sum x_i y_i }{n} - \bar{x}\bar{y} \right) \\&=& \frac{ 1 }{s_x s_y} \left( \frac{ T_{xy} }{n} - \bar{x} \bar{y} \right)\end{eqnarray}$
- 積和（2変数の積の合計）：
  $T_{xy} = \sum_{i=1}^n x_i y_i$

共分散（covariance）

共分散 $\normalsize s_{xy}$ は、偏差積和を標本数で割ったもの。
$\begin{eqnarray}s_{xy} &=& \frac{1}{n} S_{xy} \\&=& \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y}) \\&=& \frac{1}{n} \sum_{i=1}^n d_x \cdot d_y\end{eqnarray}$
- 標本数: $\normalsize n$
- 偏差: $\normalsize d_x$ , $\normalsize d_y$
共分散 $\normalsize s_{xy}$ を使うと、相関係数は次のように表せる。
$r = \frac{ s_{xy} }{s_x s_y}$

偏差平方和

偏差平方和 $\normalsize S_{xx}$ または $\normalsize S_{yy}$ は、偏差の二乗の合計を計算したもの
$\begin{eqnarray}S_{xx} &=& \sum_{i=1}^n {d_x}^2 \\&=& \sum_{i=1}^n (x_i - \bar{x})^2\end{eqnarray}$

$\begin{eqnarray}S_{yy} &=& \sum_{i=1}^n {d_y}^2 \\&=& \sum_{i=1}^n (y_i - \bar{y})^2\end{eqnarray}$
$\normalsize x$ と $\normalsize y$ についての偏差平方和 $\normalsize S_{xx}$ と $\normalsize S_{yy}$ を使うと、相関係数は次のように表せる。
$\begin{eqnarray}r &=& \frac{ S_{xy} }{ \sqrt{ S_{xx} S_{yy} } } \\&=& \frac{ \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y}) }{ \sqrt{ \sum_{i=1}^n (x_i - \bar{x})^2 \sum_{i=1}^n (y_i - \bar{y})^2 } }\end{eqnarray}$

相関関係と因果関係

相関関係から因果関係を確定するときの注意点

何でもよいから2組のデータの関係性を調べればよいわけではありません。次のような5つの因果関係が認められる場合に、相関関係を調べることが有効になります。

関連の時間性
- 原因は結果の前にあるか
関連の密接性
- 原因が結果に密接に関連するか
関連の特異性
- 原因が結果にどの程度かかわっているか
関連の普遍性
- 対象や時期、方法などが異なっていても、類似した結果が得られるか
関連の合理性
- 従来の理論や経験から考えて矛盾がないか

疑似相関（見かけの相関）

直接の相関はないが、何かある要因が2つの事象と相関しているために、 2つの事象に相関がみられるケースがあります。

このような場合を「疑似相関」といいます。つまり、相関関係があるからといって、それが必ずしも因果関係であるとは限らない場合です。

「ビアホールでの生ビールの売り上げ数」と「アイスクリーム店のお客の数」
- 2つの事象には「気温」「天候」などが相関している
「進行性の疾患をもつ患者の疾患についての知識」と「その疾患の進行度」
- 2つの事象には「疾患の内容」「治療期間」などが相関している

相関の程度

相関係数の値から、相関の程度を次のように記述できます。

-1.0≦相関係数r<-0.7	強い負の相関がある
-0.7≦相関係数r<-0.4	かなりな負の相関がある
-0.4≦相関係数r<-0.2	やや負の相関がある
-0.2≦相関係数r≦0.2	ほとんど相関がない
0.2<相関係数r≦0.4	やや正の相関がある
0.4<相関係数r≦0.7	かなりな正の相関がある
0.7<相関係数r≦1	強い正の相関がある

なお、標本数が少ない場合は、母相関係数の推定や検定（後日説明）が必要となります。

順位相関係数（rank correlation coefficient）

相関がない場合や順位に意味がある・順位だけしかわからない場合には、順位データ（データを小さいほうから並べた順位）をもとに、相関を求める方法が有効になります。

英語のテストの順位と数学のテストの順位の相関
2つの銘柄の株価の相関（経済分野）
薬と奇形児発生の相関（医学分野）

また、順位尺度のデータだけでなく、比例・間隔尺度のデータについても何らかの順位を求めることで適用できます。

スピアマン（Spearman）の順位相関係数 $\normalsize r_s$ は、相関係数と同様、次の値をとる。
$-1 \leq r_s \leq +1$
同一順位の場合は、次のように扱う（平均順位）
- 2位が2つある場合：2位と3位の中間 (2+3)/2=2.5位を順位とする
- 4位が3つある場合：4位と5位と6位の中間 (4+5+6)/3=5位を順位とする
順位相関係数は、次のようにして求められる。
$r_s = 1 - \frac{ 6 \sum_{i=1}^n {d_i}^2 }{n^3 - n}$
- 標本数: $\normalsize n$
- i 番目の順位差: $\normalsize d_i$

データ1の順位	データ2の順位	順位差 $\normalsize d$	順位差の二乗 $\normalsize d^2$
$\normalsize x_1$	$\normalsize y_1$	$\normalsize d_1 = x_1 - y_1$	$\normalsize {d_1}^2$
$\normalsize x_2$	$\normalsize y_2$	$\normalsize d_2 = x_2 - y_2$	$\normalsize {d_2}^2$
$\normalsize x_3$	$\normalsize y_3$	$\normalsize d_3 = x_3 - y_3$	$\normalsize {d_3}^2$
…	…	…	…
$\normalsize x_n$	$\normalsize y_n$	$\normalsize d_n = x_n - y_n$	$\normalsize {d_n}^2$
計		0	$\normalsize \sum_{i=1}^n {d_n}^2$

メニュー

授業内容

ケータイで教員にメール

mkawano%40ed.hyogo-dai.ac.jp

今日の5件

最新の10件

2024-04-19

2024-04-12

2023-07-14

total: 2825
today: 1
yesterday: 3
now: 4

Last-modified: Tue, 11 Mar 2014 19:49:36 JST (3692d)