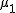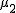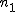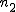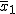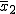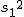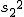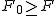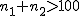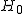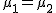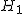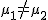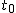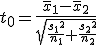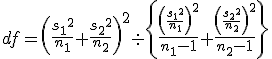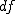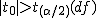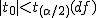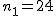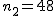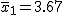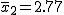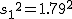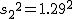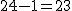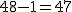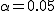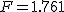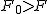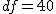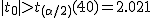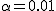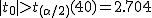対応のない2組の平均値の差の検定（母分散が未知で等しくない）

検定の対象

対応のない（独立した）2つの母集団について考える。それぞれの母数は次のとおり。ただし、母分散の値はわからない。

	母集団1	母集団2
母平均	$\normalsize \mu_1$	$\normalsize \mu_2$
標本の標本数	$\normalsize n_1$	$\normalsize n_2$
標本平均	$\normalsize \bar{x}_1$	$\normalsize \bar{x}_2$
標本分散	$\normalsize {s_1}^2$	$\normalsize {s_2}^2$

なお、標本平均は不偏分散から求める。

$s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2$

▲ ▼

等分散の検定（F検定）

等分散の検定の結果、 $\normalsize F_0 \geq F$ ならば、母分散は未知で「等しくない」場合に、この検定を使う

▲ ▼

Welchの検定

標本数の和が $\normalsize n_1 + n_2 > 100$ の場合にも使われることがある
2組の母集団の分散が2倍以上違う場合や、標本数が2倍上違う場合に使われることがあり、やや特殊な検定法である

▲ ▼

帰無仮説と対立仮説

対応のない（独立した）2組の母集団の平均に差があるかどうかを調べる。

帰無仮説 $\normalsize H_{0}$ は「2組の母集団の平均に差はない」 : $\normalsize \mu_1 = \mu_2$
対立仮説 $\normalsize H_{1}$ は「2組の母集団の平均に差がある」 : $\normalsize \mu_1 \neq \mu_2$

▲ ▼

検定統計量の算出

t分布にしたがう、検定統計量 $\normalsize t_0$ を次の式から算出する
$t_0 = \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} } }$
なお、自由度は次のように算出する（整数にならない場合は、小数点以下を切り捨て）
$df = \left( \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} \right)^2 \div \left\{ \frac{ \left( \frac{ {s_1}^2 }{n_1} \right)^2 }{n_1 - 1} + \frac{ \left( \frac{ {s_2}^2 }{n_2} \right)^2 }{n_2 - 1} \right\}$
- 自由度の計算が複雑なので、あまりおススメの方法とはいえない…

▲ ▼

仮説の判定（両側検定）

検定統計量 $\normalsize t_0$ と、自由度 $\normalsize df$ 、有意水準 $\normalsize \alpha$ の有意点の値（t分布表などから求める）を使って、判定をする
- 帰無仮説 $\normalsize H_{0}$ を棄却 : $\normalsize |t_0| > t_{(\alpha/2)}(df)$
  - 「有意に差がある」「検定の結果、有意である」「平均に差がある」
- 帰無仮説 $\normalsize H_{0}$ を採択 : $\normalsize |t_0| < t_{(\alpha/2)}(df)$
  - 「有意に差はない」「検定の結果、有意でない」「平均に差があるとはいえない」

▲ ▼

例題

女子大学生にデートに臨むときのハイヒールの高さを聞いたところ、自分を「おしゃれ」と答えた24人のハイヒールの高さの平均は3.67cm、標準偏差は1.79cmであった。また、自分を「普通」と答えた48人のハイヒールの高さの平均は2.77cm、標準偏差は1.29cmであった。「おしゃれ」と答えた人たちと「普通」と答えた人たちとでハイヒールの高さに差はあるか？

▲ ▼

考え方

自分を「おしゃれ」と答えた女子大生と自分を「普通」と答えた女子大生のハイヒールの高さについて、答えた人数やハイヒールの高さの平均と標準偏差についてまとめると、次の表のようになる。

	「おしゃれ」と答えた女子大生	「普通」と答えた女子大生
標本数	$\normalsize n_1 = 24$	$\normalsize n_2 = 48$
標本平均	$\normalsize \bar{x}_1 = 3.67$	$\normalsize \bar{x}_2 = 2.77$
標本分散	$\normalsize {s_1}^2 = 1.79^2$	$\normalsize {s_2}^2 =1.29 ^2$

まず、母分散が等しいかどうかを調べるため、等分散の検定をする。 F分布にしたがう、等分散の検定の検定統計量は、次のようになる。

$\begin{eqnarray}F_0 &=& \frac{ {1.79}^2 }{ {1.29}^2 } \\[10]&=& 1.92542\cdots \simeq 1.925\end{eqnarray}$

この値を、第1自由度が $\normalsize 24 -1 = 23$ 、第2自由度が $\normalsize 48 - 1 = 47$ 、有意水準 $\normalsize \alpha =0.05$ の F 値を分布表から調べると、 $\normalsize F=1.761$ となる。検定統計量と比較すると、 $\normalsize F_0 > F$ となり、 2組の標本の母分散は等分散ではないと判断できるので、Welchの検定を用いる。

t分布にしたがう検定統計量 $\normalsize t_0$ を求めると、次のようになる。

$\begin{eqnarray}t_0 &=& \frac{ \bar{x}_1 - \bar{x}_2 }{ \sqrt{ \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} } } \\[10]&=& \frac{ 3.67 - 2.77 }{ \sqrt{ \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} } } \\[10]&=& \frac{ 3.67 - 2.77 }{ \sqrt{ \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} } } \\[10]&=& 2.82552 \simeq 2.826\end{eqnarray}$

次に、検定のための自由度を求める。

$\begin{eqnarray}df &=& \left( \frac{ {s_1}^2 }{n_1} + \frac{ {s_2}^2 }{n_2} \right)^2 \div \left\{ \frac{ \left( \frac{ {s_1}^2 }{n_1} \right)^2 }{n_1 - 1} + \frac{ \left( \frac{ {s_2}^2 }{n_2} \right)^2 }{n_2 - 1} \right\} \\[10]&=& \left( \frac{ {1.79}^2 }{24} + \frac{ {1.29}^2 }{48} \right)^2 \div \left\{ \frac{ \left( \frac{ {1.79}^2 }{24} \right)^2 }{24 - 1} + \frac{ \left( \frac{ {1.29}^2 }{48} \right)^2 }{48 - 1} \right\} \\[10]&=& 40.019\end{eqnarray}$

整数分だけを自由度として採用すると、 $\normalsize df = 40$ となる。

この検定統計量を両側検定で判定する。有意水準 $\normalsize \alpha =0.05$ では、自由度 $\normalsize df = 40$ のt値を分布表から調べると、 $\normalsize |t_0| > t_{(\alpha/2)}(40) = 2.021$ となり、帰無仮説は棄却される。つまり、有意水準 5% で仮説検定を行った結果、 「おしゃれ」と答えた人たちと「普通」と答えた人たちとでハイヒールの高さに差がある。