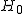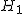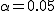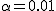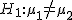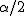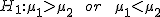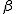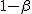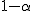健康統計の基礎・健康統計学 - 仮説検定

仮説検定

仮説検定 (Statistical hypothesis testing)

• 統計的推定 : 標本の統計量から母数を、ある一定の値（点推定）、あるいは確率的な区間（区間推定）として推測する
• 統計的検定 : 母集団に関するある仮説（予測）のもとで、標本から得られる統計量を確率を求め、仮説の正当性を判断する
  • ただし、母集団の特性（母数）の程度を推測するわけではない

仮説検定の手順

母集団に関する仮説を立てて、 その仮説が正しいという仮定のもとで、 標本の統計量が得られる確率を求め、 標本のようなことがめったに起こらない（偶然かどうか）を調べる。

1. 帰無仮説と対立仮説を立てる
2. 検定法を選択する
   • 分析目的にあった検定を分析者自身が選択する
3. 有意水準を決定する
   • 分析者自身が決定する
4. 検定統計量と有意点を算出する
   • 標本の値から検定統計量の値を算出する
   • 有意水準に対する有意点の値を算出する
5. 仮説の判定をする
   1. 検定統計量が棄却域に入っているかどうか調べる
   2. 検定統計量の値に対応するp値と有意水準を比較する

帰無仮説と対立仮説

検定では、まず検討したい母集団の特性に関する仮説を立てる。

一般には、明らかにしたい仮説を「対立仮説」(Alternative hypothesis) にして、 それに対立する仮説を「帰無仮説」(Null hypothesis) とすることが多い。 ただし、「仮説検定＝帰無仮説を棄却」することが目的ではないので注意すること。

• 帰無仮説
  • 帰無仮説に対立する仮説で、否定的な表現になる（「〜ではない」「〜と異なる」など）
  • 「母平均より標本平均のほうがおおきい」「2つの母集団の平均は等しくない」
• 対立仮説
  • 極論のような立証が難しそうで、肯定的な表現になる（「〜である」「〜と等しい」など）
  • 「母平均と標本平均は等しい」「2つの母集団の平均は等しい」

検定統計量

• 帰無仮説が正しいという仮定のもとで、標本から計算した値を、「検定統計量」という
• 検定統計量の計算式は、検定の方法によって決まっている
  • 標準正規分布やt分布のような、確率分布にしたがうような場合が多い

両側検定と片側検定

有意水準

• 正しい帰無仮説を棄却（採択しない）で、間違った対立仮説を採択するする確率を、「有意水準」(significance level) または「危険率」といい、 であらわす
  • 一般に（伝統的に） （5%）や （1%）が用いられる
• 有意水準 から、検定法に応じて確率分布表から得られた値を「有意点の値」または「限界値」という
  • 帰無仮説か棄却されるかどうかは、検定統計量と有意点の値を比較して、判定する

棄却域と採択域による判定

検定統計量（標本から算出した値）と有意点（めったに起こるかどうかの確率から算出した値）を比較することで、帰無仮説の棄却・採択を判定する。

• それぞれの検定で用いる確率分布について、次のようにして判定する
  • 有意点より外側の部分を「棄却域」といい、検定統計量が棄却域に入っている場合は、帰無仮説は棄却される
  • 有意点より内側の部分を「採択域」といい、検定統計量が採択域に入っている場合は、帰無仮説は棄却されない

たとえば、帰無仮説 を「２つ母集団の母平均が等しい」とした場合、対立仮説は2通りの場合が考えられる。

1. 対立仮説「母平均は等しくない」
   • このような場合は「両側検定」を行う
   • 棄却域は、検定に用いる確率分布の両端にある
     • 「｜検定統計量｜＞有意水準 に対応する有意点の値」なら帰無仮説は棄却
2. 対立仮説「どちらかの母平均が大きい（小さい）」
   • このような場合は「片側検定」を行う
   • 棄却域は、検定に用いる確率分布の片側にある
     • 「｜検定統計量｜＞有意水準 に対応する有意点の値」なら帰無仮説は棄却

p値による判定

検定統計量と有意水準 に対応する有意点の値を比較して判定する以外に、有意水準 を直接使って判定する方法がある。

1. 検定統計量に対応する確率（p値）を確率分布から求める
2. p値と有意水準 を比較する
   • 両側検定の場合
     • 「p値の2倍＜有意水準 」なら帰無仮説を棄却
   • 片側検定の場合
     • 「p値＜有意水準 」なら帰無仮説を棄却

母比率の検定では、確率の計算から直接p値を計算することができる。

判定結果の表現

• 帰無仮説を棄却する場合
  • 「帰無仮説を棄却する」
  • 「有意である」
  • 「対立仮説は正しい」（「絶対に」ではない）
  • 「〜でない」
• 帰無仮説を採択する場合
  • 「帰無仮説を棄却できない」
  • 「有意でない」
  • 「帰無仮説は誤っているとはいえない」
  • 「〜でないとはいえない」

帰無仮説を採択する場合に、「帰無仮説を棄却できない」といい、 「帰無仮説は正しい」といえないのは、 誤った帰無仮説を採択してしまう可能性が少なからずあるためである。 （後述の第2種の過誤のため）

第1種の過誤と第2種の過誤

• 正しい帰無仮説を棄却してしまうことを、「第一種の過誤」という
  • その確率を （つまり有意水準）であらわす
  • 仮説検定では、第1種の過誤を重視（ と の両方を小さくすることは簡単ではない）
• 間違った帰無仮説を採択してしまうことを、「第二種の過誤」という
  • その確率を であらわす
  • 間違った仮説を正しく棄却する確率を であらわし、「検定力」という
• 第一種の過誤 を小さくすると第二種の過誤 が大きくなり、第二種の過誤 を小さくすると第一種の過誤 が大きくなる関係がある
  • 第一種の過誤 も第二種の過誤 も小さくするには、標本数をできるだけ大きくするしかない

	検定の結論
	帰無仮説を棄却	帰無仮説を採択
帰無仮説は正しい	第一種の過誤 （確率 ）	正しい判断 （確率 ）
帰無仮説は間違い	正しい判断 （確率 ）	第二種の過誤 （確率 ）