Top > 2009 > 5th > Probability
AND OR

確率

▲ ▼

事象

  • あることが起こった結果を、「事象」という
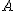    • 事象Aを \normalsize A と表す
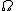    • 全体の事象のことを「全事象」といい、 \normalsize \Omega と表す
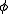    • 決して起こらないことを「空事象」といい、 \normalsize \phi と表す
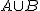    • 事象AまたはBが起こる確率を「和事象」といい、 \normalsize A \cup B と表す
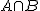    • 事象AとBが同時に起こる確率を「積事象」といい、 \normalsize A \cap B と表す
▲ ▼

確率 (Probability)

  • 「確率」とは、あることが起こる結果の割合、つまり起こりやすさの目安である
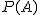    • ある事象 A が起こる確率を、 \normalsize P(A) と表す
      • 確率は、0から1の間の値をとる
        0 \leq P(A) \leq 1
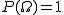    • 全事象の確率は \normalsize P( \Omega ) = 1 となる
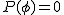    • 空事象の確率は \normalsize P( \phi ) = 0 と書く
▲ ▼

数学的確率

  • あることが起こる結果が何通りあるかを元にしてだす確率を、「数学的確率」という
  • 例えば…
    • サイコロの目の出方は6通り
    • 3の目が出る確率は 1/6
  • 事象Aの確率は、事象Aの起こる場合の数 a を、すべての場合の数（何通りあるかすべて数えたもの）N で割ったものである
    P(A) = \frac{a}{N}
▲ ▼

統計的確率

  • 実際に起こった結果を元にしてだす確率を、「統計的確率」という
  • 例えば…
    • 実際にサイコロを60回投げたら、3の目が13回出た
    • この時点での、3の目が出た確率は 13/60
  • 事象Aの確率は、事象Aの起こった回数 r を、すべての起こった回数 n で割ったものである
    P(A) = \frac{r}{n}
▲ ▼

大数の法則

  • 試行（あることを実施する）回数を増やせば増やすほど、統計的確率が数学的確率に近づいていくことを、「大数の法則」という
  • 例えば…
    • 実際にサイコロを1,000回投げたら、3の目が1,300回出た
    • その結果、3の目が出た確率はほぼ 1/3
      \begin{eqnarray}P(A) &=& \lim_{n\to\infty}\frac{r}{n}&=& \frac{a}{N}\end{eqnarray}
▲ ▼

加法定理

▲ ▼

排反前提の場合

  • 2つ、または2つ以上の排反事象（同時に起こりえない事象）が起こる確率は、 それぞれの確率の和である
    \begin{eqnarray}P(A \cup B) &=& P(A) + P(B) \\P(A \cup B \cup C \cdots ) &=& P(A) + P(B) + P(C) + \cdots \\\end{eqnarray}
    • 排反事象
      • 同時に起こりえない（2つ、または2つ以上の）事象を「排反事象」という
        A \cup B = \phi
  • 例：52枚のトランプから1枚引いたとき、ハートまたはダイヤを引く確率は、次のとおり
    \begin{eqnarray}P(A \cup B) &=& \frac{13}{52} + \frac{13}{52} \\&=& \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\end{eqnarray}
▲ ▼

一般の場合

  • 2つ、または2つ以上の事象が起こる確率は、 それぞれの確率の和から、それぞれの事象が同時に起こる確率を引いたもの
    P(A \cup B) = P(A) + P(B) - P(A \cap B)
  • 例：52枚のトランプから1枚引いたとき、ハートまたはＡ（エース）を引く確率は、次のとおり
    \begin{eqnarray}P(A \cup B) &=& \frac{13}{52} + \frac{4}{52} - \frac{1}{52} \\&=& \frac{4}{13}\end{eqnarray}
▲ ▼

乗法定理

▲ ▼

条件つき確率

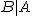  • 「Aが起こったときにBが起きる」事象を、\normalsize B \mid A と表す
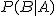  • 「Aが起こったときにBが起きる」事象の確率、つまり、Aが起こったという条件のもとでBが起きる確率を、「条件つき確率」といい、\normalsize P( B \mid A ) と表す
    \begin{eqnarray}P(B \mid A) &=& \frac{ P(A \cap B) }{ P(A) } \\\end{eqnarray}
  • 上の式の両辺に P(A) を掛けると、次のように式が変形できる
    P(B \cap A) = P(A) \times P(B \mid A)
    • BがAに関係なく起きる（事象AとBが独立な事象である）場合、「乗法定理」が導き出せる
  • 例：サイコロを投げて、奇数の目（事象A）が出たときに、それが1の目である（事象B）確率は、次のとおり
    \begin{eqnarray}P(B \mid A) &=& \frac{ P(A \cap B) }{ P(A) } \\&=& \frac{1}{3}\end{eqnarray}
    • A = 奇数の目が出る = {1, 3 ,5}
    • B = 1の目が出る = {1}
  • 例：ある男女100人について結婚しているかどうか調査した結果が、次のようになった。この100人から1人を選んだとき、それが結婚している男性である確率は？
     男性女性合計
    結婚している262147
    結婚していない292453
    合計5545100
    • A = 選んだ人が男性である = 55人
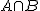    • \normalsize A \cap B = 結婚している男性である = 26
      \begin{eqnarray}P(B \mid A) &=& \frac{ P(A \cap B) }{ P(A) } \\&=& \frac{26}{55}\end{eqnarray}
▲ ▼

乗法定理

  • 2つ、または2つ以上の互いに独立な事象が同時に（または続けて）起こる確率は、 確率の積になる
    \begin{eqnarray}P(A \cap B) &=& P(A) \times P(B) \\P(A \cap B \cap C \cdots ) &=& P(A) \times P(B) \times P(C) \times \cdots \\\end{eqnarray}
  • 「独立事象」とは、ある事象の発生する確率が、他のいずれの事象の影響も受けない（他の事象に関係なく発生する事象）
  • 例：サイコロを2回投げて、2回とも1の目が出る確率（1の目が出た後、1の目が出る確率）は、次のとおり
    \begin{eqnarray}P(A \cap B) &=& \frac{1}{6} \times \frac{1}{6} \\&=& \frac{1}{36}\end{eqnarray}
▲ ▼

余事象

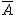  • ある事象Aについて、その事象がおこらないすべての場合（の事象）を「余事象」 \normalsize \bar{A} と表す
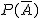  • 余事象が起こる確率を \normalsize P( \bar{A}) と表す
    P( \bar{A}) = 1 - P(A)
  • 例：サイコロを2回投げたとき、「少なくとも」1回は3の目が出る確率は、次のとおり
    1. 「少なくとも〜」の場合は、余事象の確率を考える
    2. サイコロを1回投げて、3の目が全く出ない確率は 5/6
    3. 2回目も3の目が出ない確率は、次のようになる
      \frac{5}{6} \times \frac{5}{6} = \frac{25}{36}
    4. サイコロを2回目投げて何かが出る確率（=1）から、2回とも3の目が出ない確率をひけば、少なくとも1回は3の目が出る確率になる
      1 - \frac{25}{36} = \frac{11}{36}
リロード   差分   ホーム 一覧 検索 最終更新 バックアップ リンク元   ヘルプ   最終更新のRSS
Last-modified: Tue, 11 Mar 2014 19:49:35 JST (3693d)